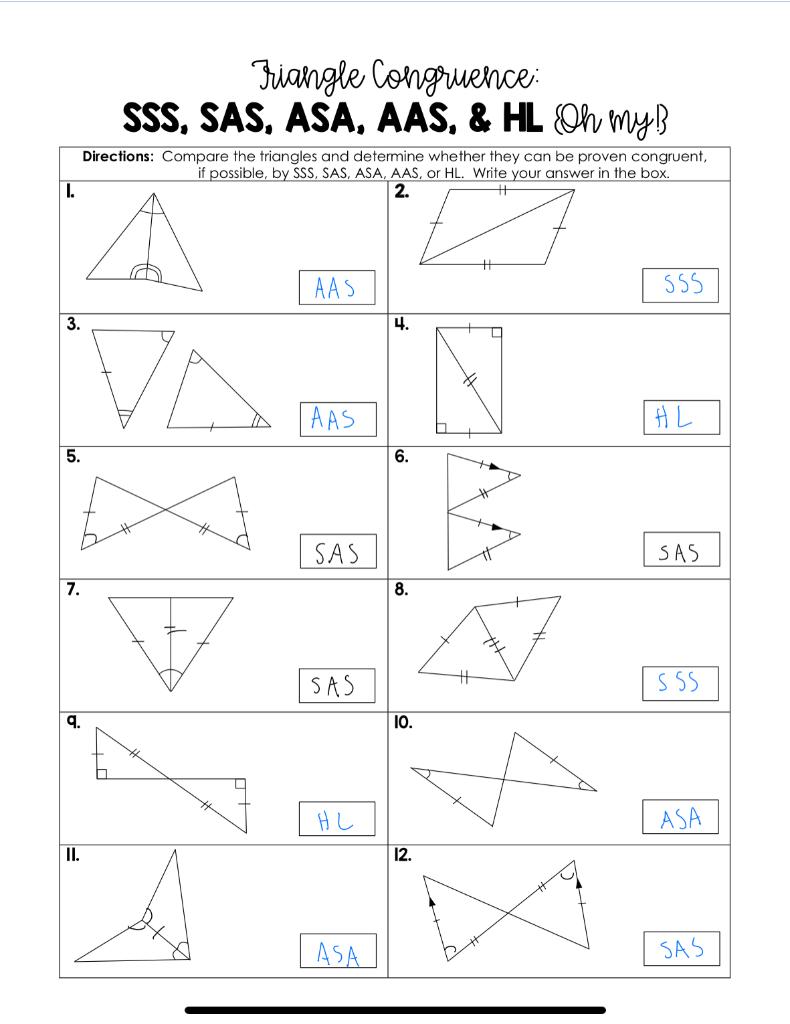
Triangle Congruence Theorems Worksheet Answer Key

Understanding Triangle Congruence Theorems
Triangle congruence theorems are a fundamental concept in geometry, allowing us to determine whether two triangles are identical in shape and size. In this blog post, we will delve into the world of triangle congruence theorems, exploring their definitions, types, and applications.
Definition of Triangle Congruence
Two triangles are said to be congruent if their corresponding sides and angles are equal. This means that if we can map one triangle onto another through a combination of translations, rotations, and reflections, then the two triangles are congruent.
Symbolic Representation
Triangle congruence is often represented using the symbol ≅. For example, ΔABC ≅ ΔDEF means that triangle ABC is congruent to triangle DEF.
Types of Triangle Congruence Theorems
There are several types of triangle congruence theorems, each with its own set of conditions and criteria. Some of the most common types include:
- Side-Side-Side (SSS) Congruence Theorem: If three sides of one triangle are equal to the corresponding sides of another triangle, then the two triangles are congruent.
- Side-Angle-Side (SAS) Congruence Theorem: If two sides and the included angle of one triangle are equal to the corresponding sides and angle of another triangle, then the two triangles are congruent.
- Angle-Side-Angle (ASA) Congruence Theorem: If two angles and the included side of one triangle are equal to the corresponding angles and side of another triangle, then the two triangles are congruent.
- Angle-Angle-Side (AAS) Congruence Theorem: If two angles and a non-included side of one triangle are equal to the corresponding angles and side of another triangle, then the two triangles are congruent.
- Hypotenuse-Leg (HL) Congruence Theorem: If the hypotenuse and a leg of one right triangle are equal to the corresponding hypotenuse and leg of another right triangle, then the two triangles are congruent.
Worksheet Answer Key
The following is a sample worksheet answer key for triangle congruence theorems:
| Problem | Answer |
|---|---|
| ΔABC and ΔDEF have sides AB = 5, BC = 6, and AC = 7. If DE = 5, EF = 6, and DF = 7, are the triangles congruent? | Yes, by SSS Congruence Theorem |
| ΔGHI and ΔJKL have angles ∠G = 30°, ∠H = 60°, and ∠I = 90°. If ∠J = 30°, ∠K = 60°, and ∠L = 90°, are the triangles congruent? | No, there is not enough information to determine congruence |
| ΔMNO and ΔPQR have sides MN = 8, NO = 15, and MO = 17. If PQ = 8, QR = 15, and PR = 17, are the triangles congruent? | Yes, by SSS Congruence Theorem |
Conclusion
Triangle congruence theorems are a fundamental concept in geometry, allowing us to determine whether two triangles are identical in shape and size. By understanding the different types of triangle congruence theorems, including SSS, SAS, ASA, AAS, and HL, we can apply these theorems to a wide range of problems and situations.
What is triangle congruence?
+Triangle congruence is the concept of two triangles having the same shape and size.
What are the different types of triangle congruence theorems?
+There are five main types of triangle congruence theorems: SSS, SAS, ASA, AAS, and HL.
How do I determine if two triangles are congruent?
+You can determine if two triangles are congruent by using the different types of triangle congruence theorems, such as SSS, SAS, ASA, AAS, and HL.
Related Terms:
- ASA and AAS Congruence Worksheet