Transform Your Math Skills with Algebra 2 Transformations
Algebra 2 transformations are a crucial concept in mathematics, and understanding them can significantly enhance your math skills. Transformations involve changing the position, size, or shape of a graph or figure, and they play a vital role in various mathematical disciplines, including geometry, trigonometry, and calculus. In this article, we will delve into the world of Algebra 2 transformations, exploring the different types, their applications, and providing examples to help you grasp the concept.
What are Algebra 2 Transformations?
In Algebra 2, transformations refer to the process of altering the graph or equation of a function to create a new graph or equation. These transformations can be applied to various types of functions, including linear, quadratic, polynomial, and rational functions. The primary goal of transformations is to change the position, size, or shape of the graph, which can help in solving equations, graphing functions, and modeling real-world problems.
Types of Algebra 2 Transformations
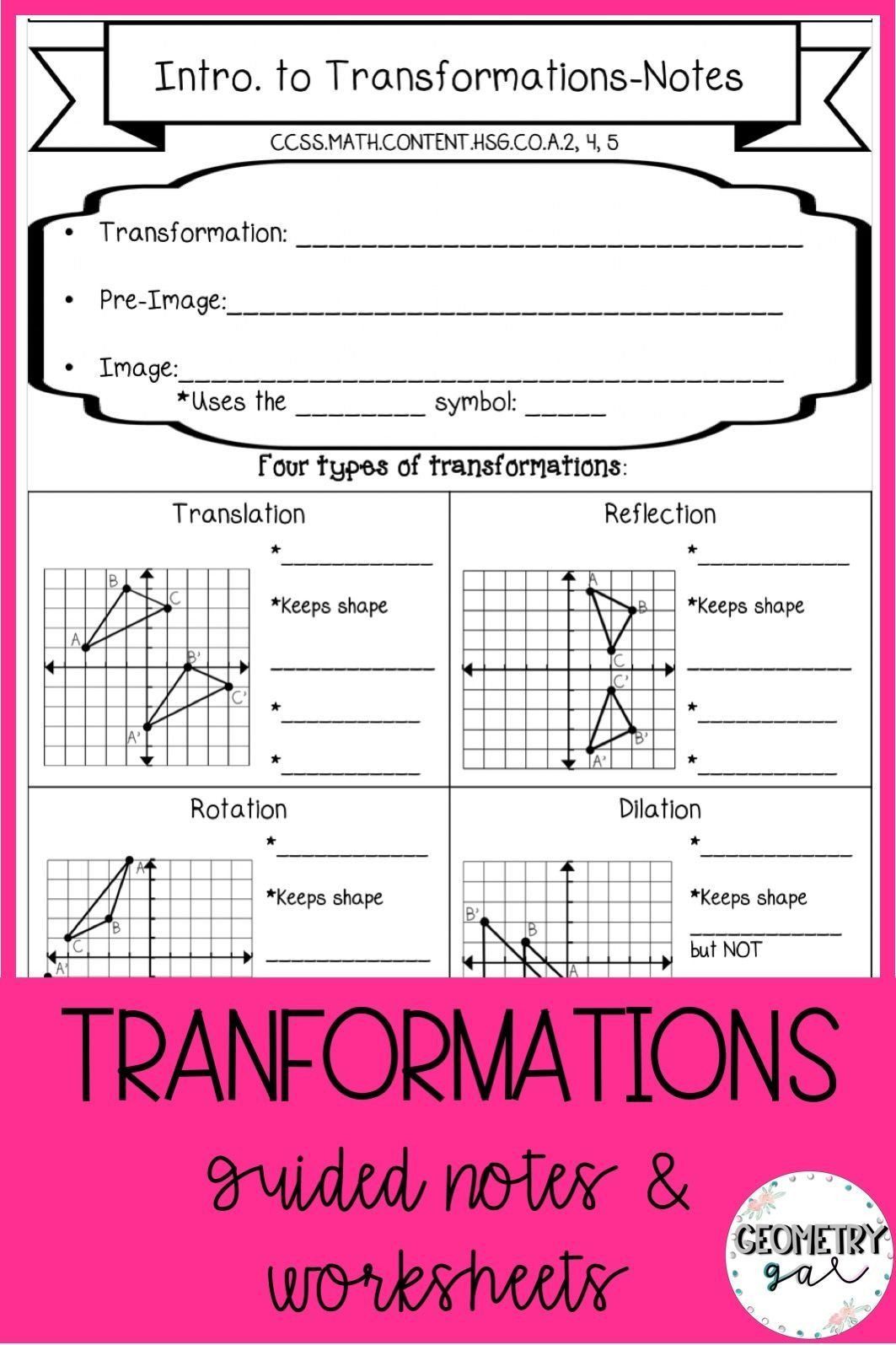
There are several types of transformations in Algebra 2, including:
- Translations: A translation involves moving the graph of a function horizontally or vertically. For example, if we have a function f(x) = x^2, we can translate it horizontally by replacing x with x - 2 to get the new function f(x) = (x - 2)^2.
- Reflections: A reflection involves flipping the graph of a function over the x-axis, y-axis, or the line y = x. For instance, if we have a function f(x) = x^2, we can reflect it over the x-axis by replacing f(x) with -f(x) to get the new function f(x) = -x^2.
- Rotations: A rotation involves rotating the graph of a function by a certain angle around the origin. For example, if we have a function f(x) = x^2, we can rotate it by 90 degrees counterclockwise to get the new function f(x) = x^2 / 2.
- Dilations: A dilation involves stretching or shrinking the graph of a function horizontally or vertically. For instance, if we have a function f(x) = x^2, we can dilate it horizontally by replacing x with 2x to get the new function f(x) = (2x)^2.
- Glide Reflections: A glide reflection involves combining a translation and a reflection. For example, if we have a function f(x) = x^2, we can glide reflect it over the x-axis and then translate it horizontally by 2 units to get the new function f(x) = -(x - 2)^2.
Applications of Algebra 2 Transformations
Transformations have numerous applications in mathematics and real-world problems. Some of the key applications include:
- Graphing Functions: Transformations can help in graphing functions by altering the position, size, or shape of the graph.
- Solving Equations: Transformations can aid in solving equations by simplifying the equation or changing its form.
- Modeling Real-World Problems: Transformations can be used to model real-world problems, such as the motion of objects, population growth, and financial transactions.
- Computer Science: Transformations are essential in computer science, particularly in computer graphics, game development, and image processing.
Examples of Algebra 2 Transformations
Here are some examples of Algebra 2 transformations:
- Example 1: If we have a function f(x) = x^2, we can translate it horizontally by 2 units to get the new function f(x) = (x - 2)^2.
- Example 2: If we have a function f(x) = x^2, we can reflect it over the x-axis to get the new function f(x) = -x^2.
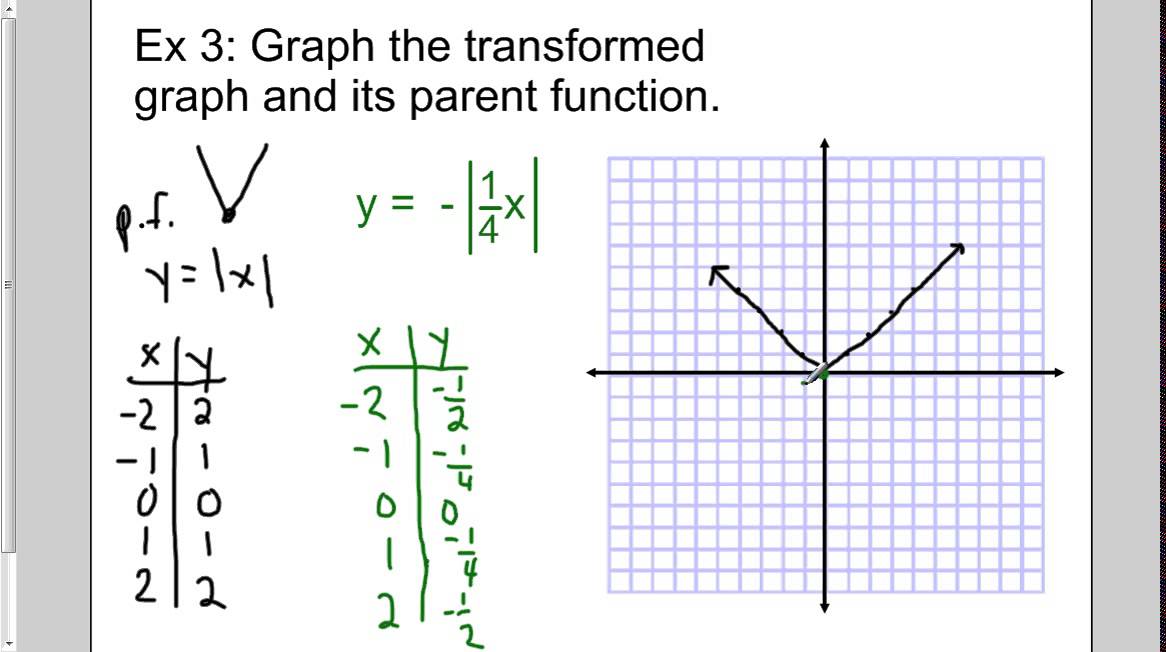
- Example 3: If we have a function f(x) = x^2, we can dilate it horizontally by a factor of 2 to get the new function f(x) = (2x)^2.
| Original Function | Transformation | New Function |
|---|---|---|
| f(x) = x^2 | Translate horizontally by 2 units | f(x) = (x - 2)^2 |
| f(x) = x^2 | Reflect over the x-axis | f(x) = -x^2 |
| f(x) = x^2 | Dilate horizontally by a factor of 2 | f(x) = (2x)^2 |
📝 Note: When performing transformations, it's essential to understand the properties of the function and how it will be affected by the transformation.
Conclusion
Algebra 2 transformations are a powerful tool in mathematics, enabling you to alter the position, size, or shape of a graph or figure. By understanding the different types of transformations and their applications, you can enhance your math skills and tackle complex problems with ease. Remember to practice transformations regularly to become proficient in applying them to various mathematical disciplines.
What are the main types of Algebra 2 transformations?
+The main types of Algebra 2 transformations are translations, reflections, rotations, dilations, and glide reflections.
How do transformations help in graphing functions?
+Transformations can help in graphing functions by altering the position, size, or shape of the graph, making it easier to visualize and analyze the function.
What are some real-world applications of Algebra 2 transformations?
+Algebra 2 transformations have numerous real-world applications, including modeling population growth, financial transactions, and the motion of objects.
Related Terms:
- Parent Functions and Transformations worksheet
- Transformations of functions Worksheet pdf
- Algebra 1 transformations Worksheet PDF



