Transforming Parent Functions: A Math Worksheet Guide
Understanding Parent Functions and Their Transformations
Parent functions are the most basic functions in mathematics, and they serve as the foundation for more complex functions. These functions can be transformed in various ways to create new functions, which is essential in problem-solving and modeling real-world phenomena. In this guide, we will explore the concept of parent functions, their transformations, and provide a comprehensive worksheet to help you practice and reinforce your understanding.
What Are Parent Functions?
Parent functions are the simplest functions in mathematics, and they can be broadly classified into several categories, including:
- Linear functions: These functions have a constant rate of change and can be represented by a straight line.
- Quadratic functions: These functions have a parabolic shape and can be represented by a quadratic equation.
- Exponential functions: These functions have a constant rate of growth or decay and can be represented by an exponential equation.
- Logarithmic functions: These functions have a logarithmic shape and can be represented by a logarithmic equation.
Some common examples of parent functions include:
- f(x) = x (linear function)
- f(x) = x^2 (quadratic function)
- f(x) = 2^x (exponential function)
- f(x) = log(x) (logarithmic function)
Transforming Parent Functions
Parent functions can be transformed in various ways to create new functions. These transformations can be classified into several categories, including:
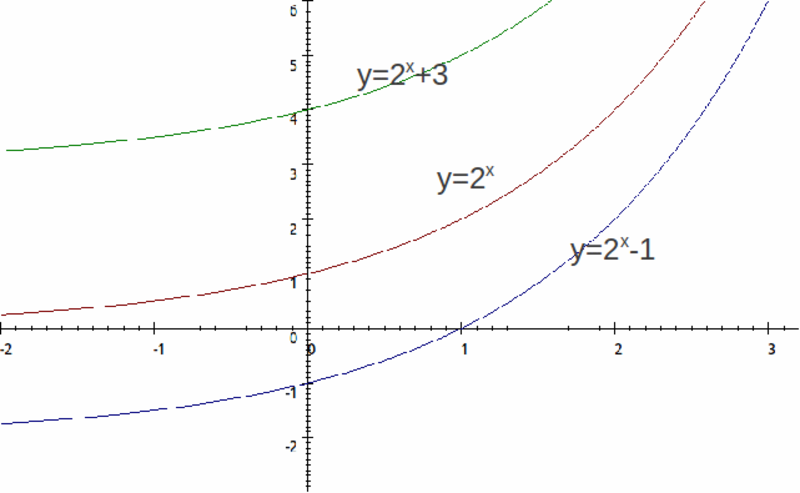
- Vertical shifts: These occur when a constant is added or subtracted from the parent function, causing it to shift up or down.
- Horizontal shifts: These occur when a constant is added or subtracted from the input of the parent function, causing it to shift left or right.
- Reflections: These occur when the parent function is reflected across the x-axis or y-axis.
- Stretches and compressions: These occur when the parent function is stretched or compressed horizontally or vertically.
Some examples of transformed parent functions include:
- f(x) = x + 2 (vertical shift)
- f(x) = (x - 3)^2 (horizontal shift)
- f(x) = -x^2 (reflection across the x-axis)
- f(x) = 2x^2 (vertical stretch)
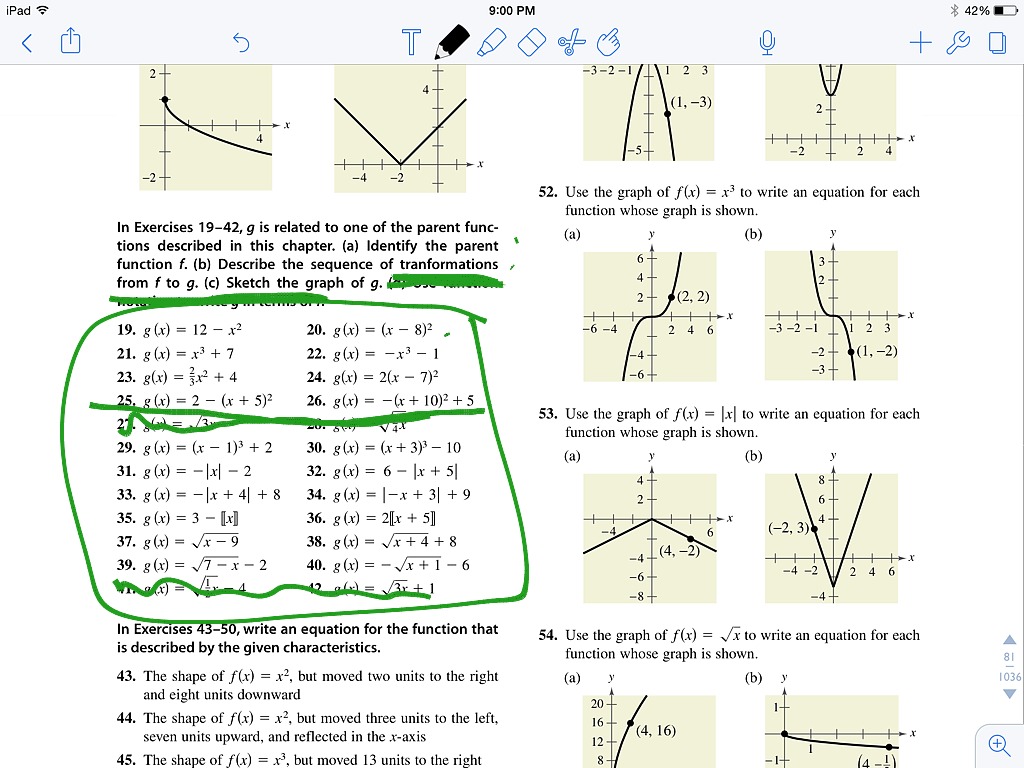
Worksheet: Transforming Parent Functions
The following worksheet provides a comprehensive set of exercises to help you practice transforming parent functions.
| Problem | Solution |
|---|---|
| 1. If f(x) = x^2, find f(x + 2). | f(x + 2) = (x + 2)^2 |
| 2. If f(x) = 2^x, find f(x - 1). | f(x - 1) = 2^(x - 1) |
| 3. If f(x) = x, find f(-x). | f(-x) = -x |
| 4. If f(x) = x^2, find f(2x). | f(2x) = (2x)^2 = 4x^2 |
| 5. If f(x) = log(x), find f(x + 1). | f(x + 1) = log(x + 1) |
Conclusion
In this guide, we have explored the concept of parent functions and their transformations. We have also provided a comprehensive worksheet to help you practice and reinforce your understanding. Remember, mastering parent functions and their transformations is essential for problem-solving and modeling real-world phenomena.
What is a parent function?
+A parent function is the most basic function in mathematics, and it serves as the foundation for more complex functions.
What are some common examples of parent functions?
+Some common examples of parent functions include f(x) = x, f(x) = x^2, f(x) = 2^x, and f(x) = log(x).
What are some common transformations of parent functions?
+Some common transformations of parent functions include vertical shifts, horizontal shifts, reflections, and stretches and compressions.



