5 Ways to Calculate Surface Area of Prisms
Understanding the Concept of Surface Area
The surface area of a three-dimensional object is the total area of its surface. For prisms, which are polyhedra with two identical faces that are parallel and oriented in the same direction, calculating the surface area involves finding the area of each face and summing them up. This article will explore five methods to calculate the surface area of prisms, highlighting their formulas and applications.
Method 1: Rectangular Prism - Perimeter and Height
For a rectangular prism, the surface area (SA) can be calculated using the formula:
SA = 2lw + 2lh + 2wh
Where: - l is the length of the prism - w is the width of the prism - h is the height of the prism
This method involves finding the perimeter of the base and multiplying it by the height, then adding the areas of the top and bottom faces.
📝 Note: This method is straightforward and useful for simple rectangular prisms.
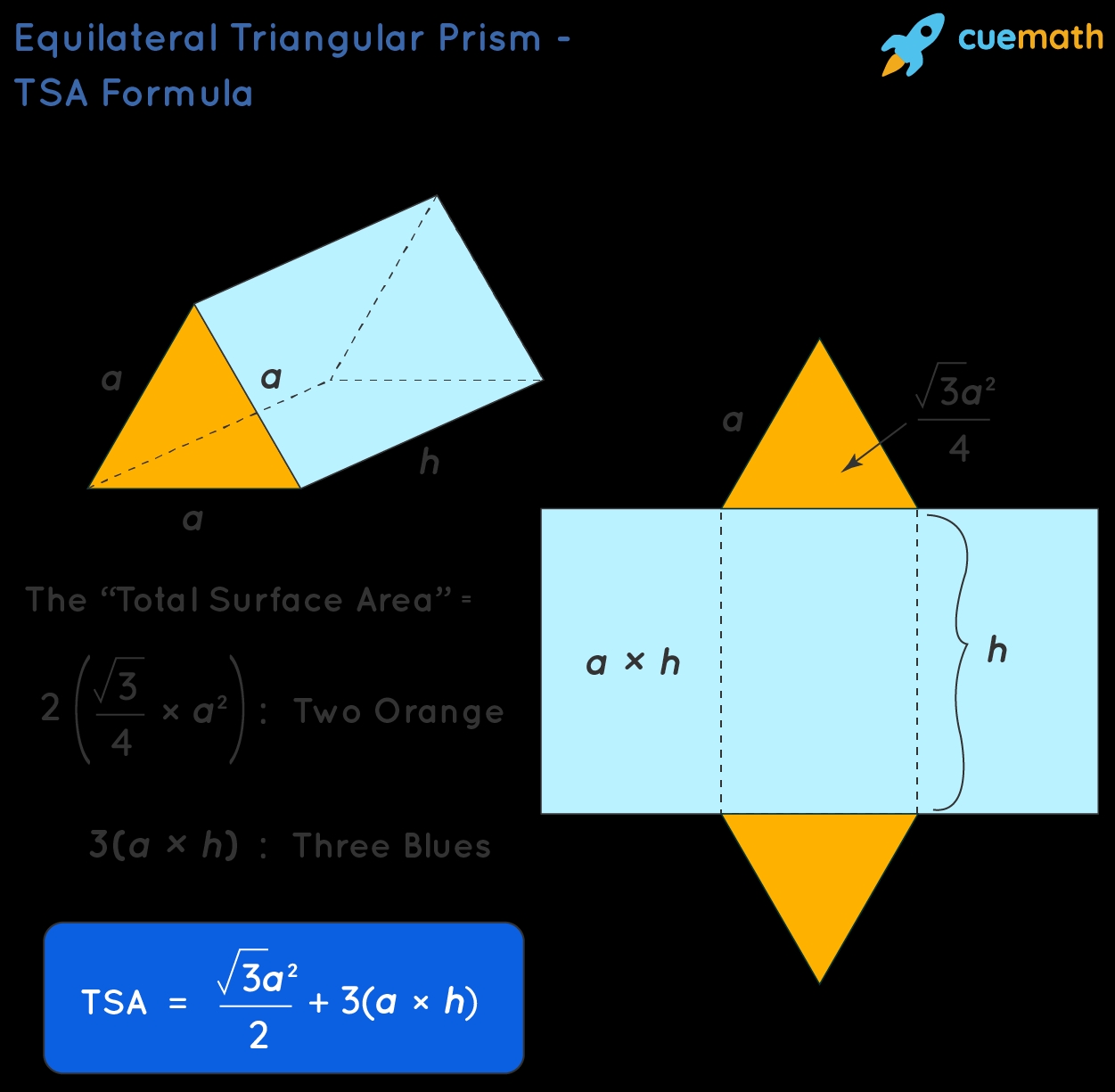
Method 2: Triangular Prism - Base and Height
For a triangular prism, the surface area can be calculated using the formula:
SA = bh + 3 × (0.5 × b × h)
Where: - b is the base length of the triangle - h is the height of the prism - 0.5 × b × h is the area of one triangular face
This method involves finding the area of the base and adding the areas of the three triangular faces.
📝 Note: This method requires the base length and height to calculate the surface area.
Method 3: Pentagon Prism - Apothem and Perimeter
For a pentagonal prism, the surface area can be calculated using the formula:
SA = 5 × (0.5 × a × p) + 2 × (0.5 × a × p)
Where: - a is the apothem of the pentagon (distance from center to a vertex) - p is the perimeter of the pentagon
This method involves finding the area of one pentagonal face and multiplying it by 5, then adding the areas of the top and bottom faces.
📝 Note: This method requires the apothem and perimeter to calculate the surface area.
Method 4: Hexagonal Prism - Apothem and Perimeter
For a hexagonal prism, the surface area can be calculated using the formula:
SA = 6 × (0.5 × a × p) + 2 × (0.5 × a × p)
Where: - a is the apothem of the hexagon (distance from center to a vertex) - p is the perimeter of the hexagon
This method involves finding the area of one hexagonal face and multiplying it by 6, then adding the areas of the top and bottom faces.
📝 Note: This method requires the apothem and perimeter to calculate the surface area.
Method 5: General Prism - Lateral Area and Base Area
For any prism, the surface area can be calculated using the formula:
SA = LA + 2BA
Where: - LA is the lateral area (area of the side faces) - BA is the base area (area of the top and bottom faces)
This method involves finding the lateral area and adding twice the base area to get the total surface area.
📝 Note: This method is a general approach that can be applied to any prism.
| Method | Formula | Description |
|---|---|---|
| Rectangular Prism | SA = 2lw + 2lh + 2wh | Perimeter and height |
| Triangular Prism | SA = bh + 3 × (0.5 × b × h) | Base and height |
| Pentagon Prism | SA = 5 × (0.5 × a × p) + 2 × (0.5 × a × p) | Apothem and perimeter |
| Hexagonal Prism | SA = 6 × (0.5 × a × p) + 2 × (0.5 × a × p) | Apothem and perimeter |
| General Prism | SA = LA + 2BA | Lateral area and base area |
In summary, calculating the surface area of prisms involves finding the area of each face and summing them up. The five methods presented above provide different approaches to calculating the surface area, depending on the shape and dimensions of the prism. By understanding these methods, you can accurately calculate the surface area of various prisms.
What is the surface area of a rectangular prism with a length of 5 cm, width of 3 cm, and height of 2 cm?
+SA = 2lw + 2lh + 2wh = 2(5)(3) + 2(5)(2) + 2(3)(2) = 30 + 20 + 12 = 62 cm²
What is the surface area of a triangular prism with a base length of 4 cm, height of 3 cm, and slant height of 5 cm?
+SA = bh + 3 × (0.5 × b × h) = (4)(3) + 3 × (0.5 × 4 × 3) = 12 + 18 = 30 cm²
What is the surface area of a pentagonal prism with an apothem of 2 cm, perimeter of 10 cm, and height of 4 cm?
+SA = 5 × (0.5 × a × p) + 2 × (0.5 × a × p) = 5 × (0.5 × 2 × 10) + 2 × (0.5 × 2 × 10) = 50 + 20 = 70 cm²
Related Terms:
- Surface Area worksheet answers
- Surface area of cylinder worksheet