Surface Area Nets Worksheet
Understanding Surface Area Nets
Surface area nets are a great way to visualize and calculate the surface area of 3D shapes. In this worksheet, we’ll explore what surface area nets are, how to identify them, and how to use them to calculate the surface area of different shapes.
What are Surface Area Nets?
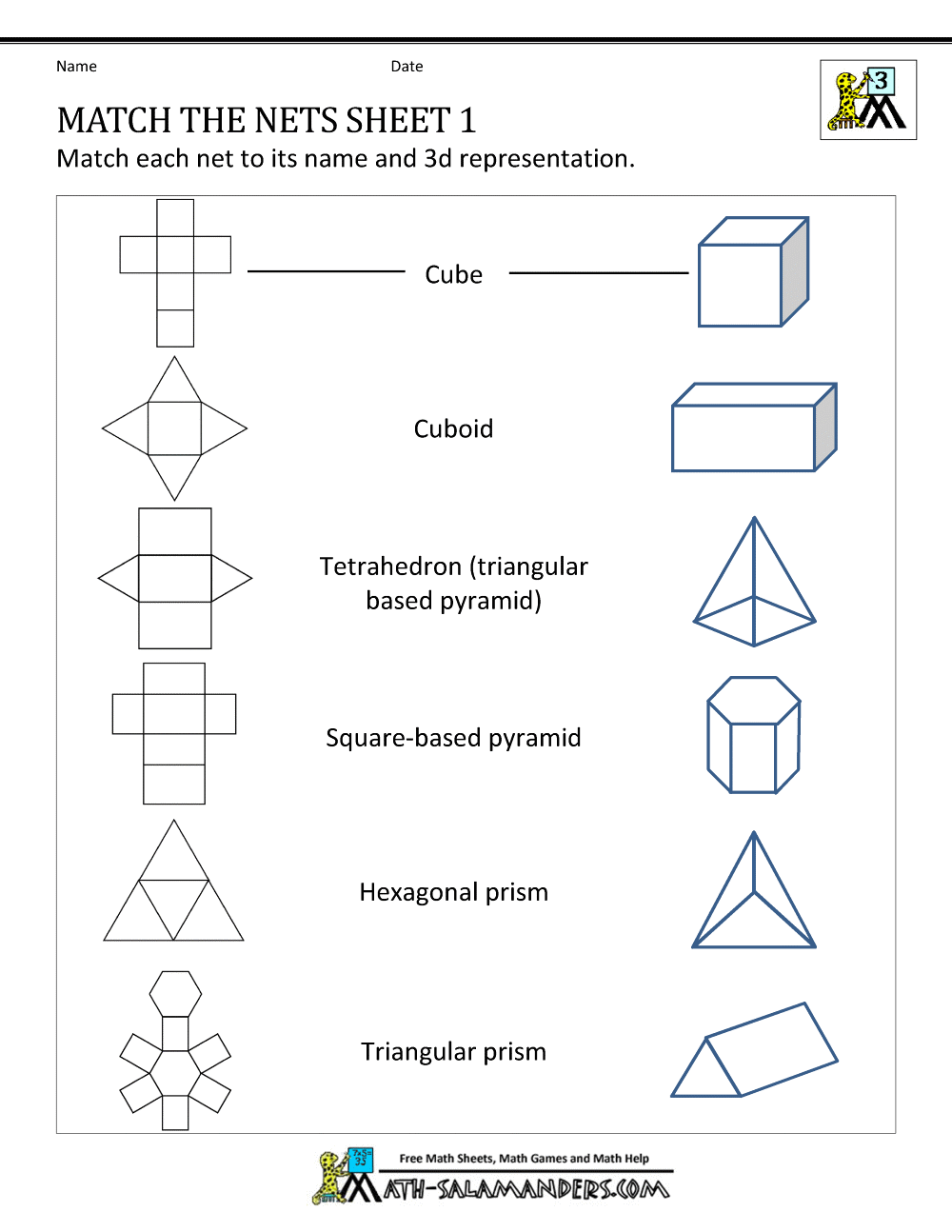
A surface area net is a 2D representation of a 3D shape, showing all the faces of the shape as a flat net. It’s called a “net” because it’s a network of faces that can be folded up to form the original 3D shape.
📝 Note: Surface area nets are also known as "polyhedral nets" or simply "nets".
Types of Surface Area Nets
There are several types of surface area nets, including:
- Rectangular prism net
- Triangular prism net
- Pyramid net
- Cylinder net
- Cone net
Each type of net has its own unique characteristics and is used to represent a specific type of 3D shape.
How to Identify Surface Area Nets
To identify a surface area net, look for the following characteristics:
- A flat, 2D representation of a 3D shape
- A network of faces that can be folded up to form the original shape
- All faces are connected at their edges
Calculating Surface Area using Nets
To calculate the surface area of a 3D shape using a net, follow these steps:
- Identify the shape and its corresponding net
- Count the number of faces on the net
- Calculate the area of each face
- Add up the areas of all the faces to get the total surface area
Examples and Practice
Here are a few examples to practice identifying and calculating surface area using nets:
- Rectangular Prism Net
- Calculate the surface area of a rectangular prism with a length of 6 cm, a width of 4 cm, and a height of 2 cm.
- Net:
- 2 x 6 cm x 4 cm faces
- 2 x 6 cm x 2 cm faces
- 2 x 4 cm x 2 cm faces
- Surface Area: 2(6 x 4) + 2(6 x 2) + 2(4 x 2) = 112 cm^2
- Triangular Prism Net
- Calculate the surface area of a triangular prism with a base area of 12 cm^2 and a height of 5 cm.
- Net:
- 2 x 12 cm^2 triangular faces
- 3 x 5 cm x 4 cm rectangular faces
- Surface Area: 2 x 12 + 3 x 5 x 4 = 96 cm^2
📝 Note: Make sure to count the number of faces and calculate the area of each face carefully to get the correct surface area.
Table of Surface Area Formulas
Here is a table of surface area formulas for different shapes:
| Shape | Surface Area Formula |
|---|---|
| Rectangular Prism | 2lw + 2lh + 2wh |
| Triangular Prism | 2B + 3lh |
| Pyramid | B + \frac{1}{2}pl |
| Cylinder | 2πrh + 2πr^2 |
| Cone | πr^2 + πrl |
Conclusion
Surface area nets are a powerful tool for visualizing and calculating the surface area of 3D shapes. By understanding how to identify and use nets, you can easily calculate the surface area of different shapes. Remember to count the number of faces and calculate the area of each face carefully to get the correct surface area.
What is a surface area net?
+A surface area net is a 2D representation of a 3D shape, showing all the faces of the shape as a flat net.
How do I calculate surface area using a net?
+To calculate surface area using a net, count the number of faces, calculate the area of each face, and add up the areas of all the faces.
What are some common types of surface area nets?
+Some common types of surface area nets include rectangular prism nets, triangular prism nets, pyramid nets, cylinder nets, and cone nets.
Related Terms:
- teacher synergy llc
- Khan Academy
- IXL
- BrainPOP
- Udacity
- Duolingo