Special Right Triangles Worksheet Answer Key Made Easy
Unlocking the Secrets of Special Right Triangles
When it comes to geometry, special right triangles are a fundamental concept that can be a bit tricky to grasp. However, with the right approach and practice, you can become a master of these triangles in no time. In this article, we will delve into the world of special right triangles, explore their properties, and provide you with a comprehensive worksheet answer key to help you practice and improve your skills.
What are Special Right Triangles?
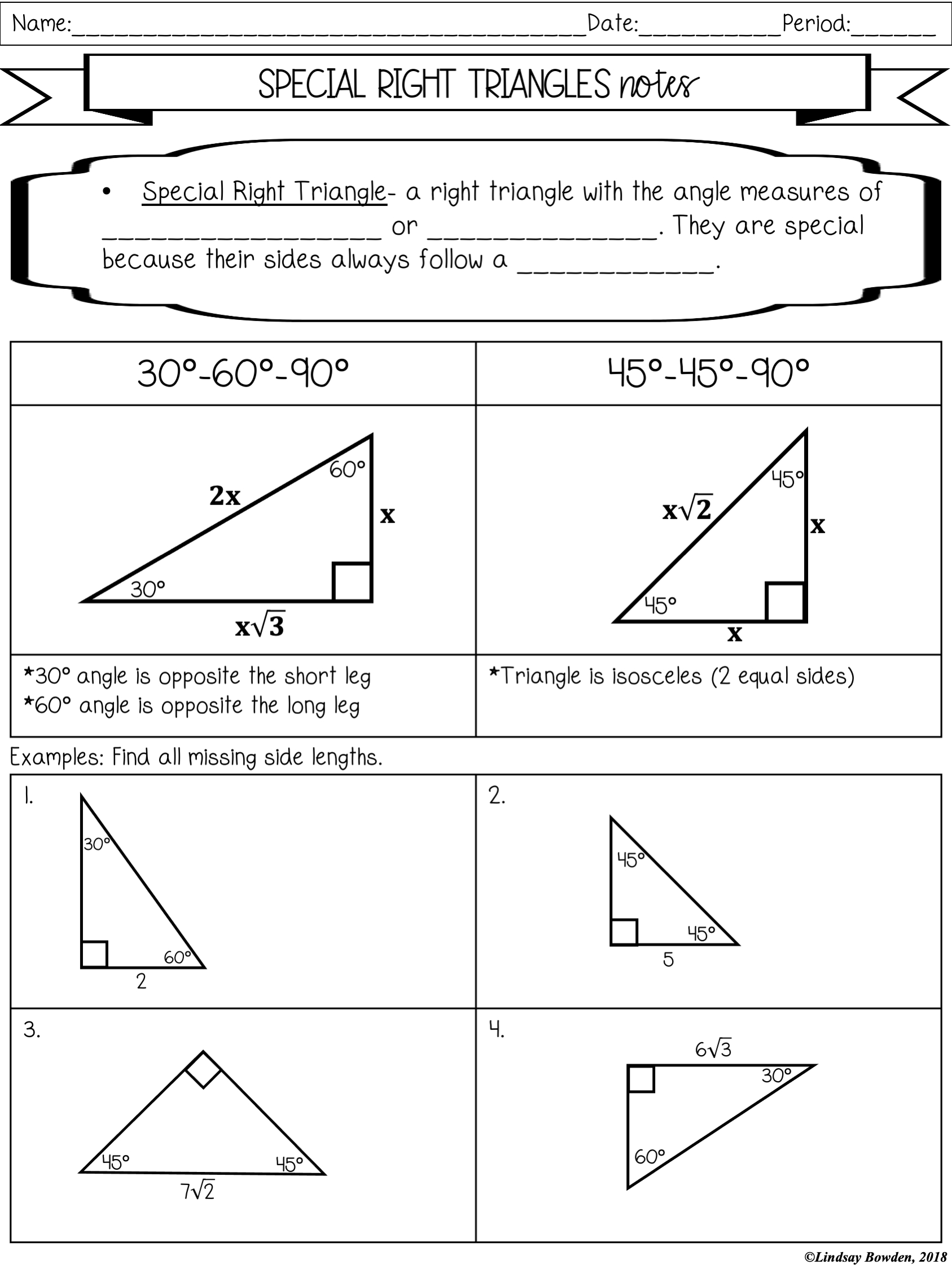
Special right triangles are right-angled triangles with specific angle measures that make them unique and useful in various mathematical and real-world applications. The two most common types of special right triangles are the 45-45-90 triangle and the 30-60-90 triangle.
45-45-90 Triangle
A 45-45-90 triangle is a right triangle with two 45-degree angles and one 90-degree angle. The sides of this triangle are in the ratio of 1:1:√2, where the hypotenuse is √2 times the length of the legs.
🤔 Note: The legs of a 45-45-90 triangle are congruent, meaning they are equal in length.
30-60-90 Triangle
A 30-60-90 triangle is a right triangle with one 30-degree angle, one 60-degree angle, and one 90-degree angle. The sides of this triangle are in the ratio of 1:√3:2, where the hypotenuse is 2 times the length of the shorter leg.
🤔 Note: The shorter leg of a 30-60-90 triangle is half the length of the hypotenuse.
Properties of Special Right Triangles
Special right triangles have several properties that make them useful in various mathematical applications. Some of these properties include:
- Side ratios: The sides of special right triangles are in specific ratios, making it easy to find missing side lengths.
- Angle bisectors: The angle bisectors of special right triangles divide the opposite side into segments that are proportional to the other two sides.
- Median relationships: The medians of special right triangles are related to the side lengths in specific ways.
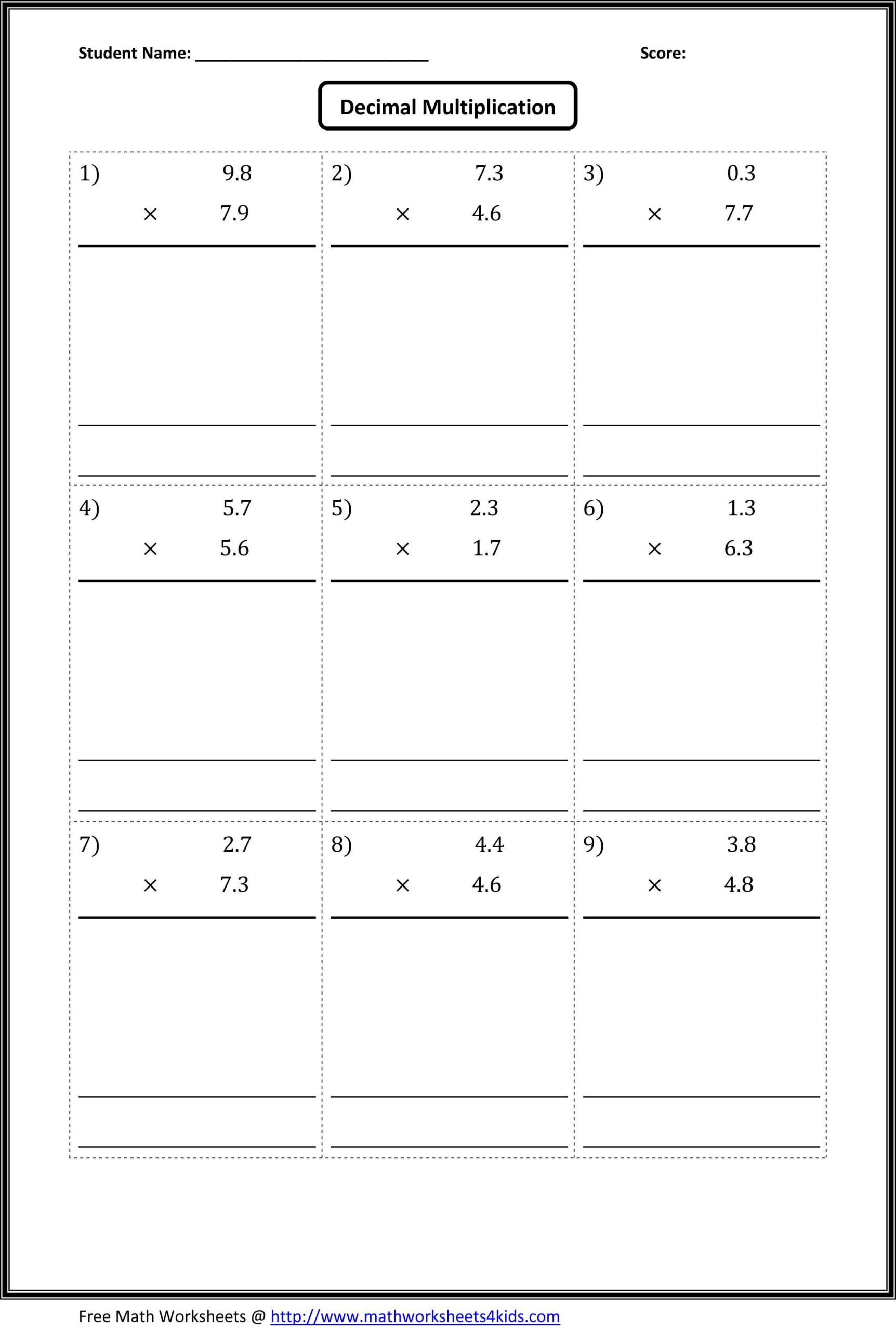
Worksheet Answer Key
Here is a comprehensive worksheet answer key to help you practice and improve your skills with special right triangles:

| Problem | Answer |
|---|---|
| 1. In a 45-45-90 triangle, if the legs are 5 inches long, what is the length of the hypotenuse? | 5√2 inches |
| 2. In a 30-60-90 triangle, if the shorter leg is 6 inches long, what is the length of the hypotenuse? | 12 inches |
| 3. In a 45-45-90 triangle, if the hypotenuse is 10 inches long, what is the length of the legs? | 5√2 inches |
| 4. In a 30-60-90 triangle, if the longer leg is 12 inches long, what is the length of the shorter leg? | 6 inches |
| 5. In a 45-45-90 triangle, if the legs are 8 inches long, what is the length of the hypotenuse? | 8√2 inches |
Conclusion
Special right triangles are an essential concept in geometry, and with practice and patience, you can become proficient in working with them. By understanding the properties and side ratios of these triangles, you can solve a wide range of problems and applications. Remember to practice regularly and use the worksheet answer key provided to improve your skills.
What is the difference between a 45-45-90 triangle and a 30-60-90 triangle?
+A 45-45-90 triangle has two 45-degree angles and one 90-degree angle, while a 30-60-90 triangle has one 30-degree angle, one 60-degree angle, and one 90-degree angle.
What is the side ratio of a 45-45-90 triangle?
+The side ratio of a 45-45-90 triangle is 1:1:√2, where the hypotenuse is √2 times the length of the legs.
What is the side ratio of a 30-60-90 triangle?
+The side ratio of a 30-60-90 triangle is 1:√3:2, where the hypotenuse is 2 times the length of the shorter leg.
Related Terms:
- Special Right Triangles Worksheet pdf
- Special right triangles Notes
- Special right triangles formula
- Multi step Special Right Triangles