Master 30-60-90 Triangles in 5 Easy Steps

Unlocking the Secrets of 30-60-90 Triangles
For many students, 30-60-90 triangles can be a daunting concept to grasp, but with the right approach, it can become a straightforward and even enjoyable topic. In this article, we will break down the process of mastering 30-60-90 triangles into 5 easy steps. By following these steps, you'll be well on your way to becoming a pro at solving these triangles.
Step 1: Understanding the Basics
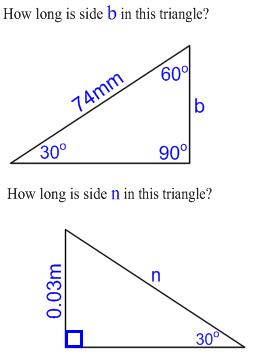
A 30-60-90 triangle is a special type of right triangle where one angle measures 30 degrees, another angle measures 60 degrees, and the third angle is a right angle (90 degrees). These triangles are also known as 30-60-90 right triangles. The side opposite the 30-degree angle is the shortest side, the side opposite the 60-degree angle is the medium side, and the hypotenuse (the side opposite the right angle) is the longest side.
Key Ratios to Remember
In a 30-60-90 triangle, the ratio of the lengths of the sides is always the same. The ratio is:
- 1:√3:2
This means that if the shortest side (opposite the 30-degree angle) is 1 unit long, the medium side (opposite the 60-degree angle) is √3 units long, and the hypotenuse is 2 units long.
Step 2: Learning the Patterns
One of the easiest ways to master 30-60-90 triangles is to recognize the patterns. These triangles always follow the same pattern, which is:
- 30-60-90 triangle pattern:
| Side | Length |
|---|---|
| Shortest side (30°) | 1x |
| Medium side (60°) | √3x |
| Hypotenuse (90°) | 2x |
Where x is a multiplier.
Step 3: Applying the Patterns
Now that you've learned the pattern, it's time to apply it. Let's say you're given a 30-60-90 triangle with a shortest side of length 6. Using the pattern, you can calculate the length of the medium side and the hypotenuse:
- Medium side: 6√3
- Hypotenuse: 12
As you can see, the pattern makes it easy to find the lengths of the sides.
📝 Note: Remember to always simplify the radical expressions (e.g., 6√3 instead of 6 * √3).
Step 4: Solving Problems
Now it's time to put your knowledge to the test! Let's say you're given a 30-60-90 triangle with a hypotenuse of length 24. Using the pattern, you can calculate the length of the shortest side and the medium side:
- Shortest side: 12
- Medium side: 12√3
As you can see, solving problems involving 30-60-90 triangles is a breeze once you've mastered the pattern.
Step 5: Practicing, Practicing, Practicing
The final step is the most important one: practice! The more you practice solving 30-60-90 triangles, the more comfortable you'll become with the pattern and the easier it will be to recognize and solve these triangles.
Practice Exercises
- Solve the following 30-60-90 triangle problems:
- If the shortest side is 8, what is the length of the medium side and the hypotenuse?
- If the hypotenuse is 36, what is the length of the shortest side and the medium side?
- If the medium side is 15√3, what is the length of the shortest side and the hypotenuse?
📝 Note: Try to solve these exercises on your own before checking the answers.
What is the ratio of the lengths of the sides in a 30-60-90 triangle?
+The ratio of the lengths of the sides in a 30-60-90 triangle is 1:√3:2.
How do I find the length of the medium side in a 30-60-90 triangle?
+To find the length of the medium side, multiply the length of the shortest side by √3.
What is the pattern for a 30-60-90 triangle?
+The pattern for a 30-60-90 triangle is:
| Side | Length |
|---|---|
| Shortest side (30°) | 1x |
| Medium side (60°) | √3x |
| Hypotenuse (90°) | 2x |
In conclusion, mastering 30-60-90 triangles is a matter of understanding the basics, learning the patterns, applying the patterns, solving problems, and practicing, practicing, practicing. With these 5 easy steps, you’ll be well on your way to becoming a pro at solving these triangles. Remember to always practice and apply what you’ve learned to reinforce your understanding. Happy solving!