Solving Radical Equations Made Easy

Understanding Radical Equations
Radical equations are equations that contain radicals, which are mathematical expressions that involve the square root or other roots of a number. These equations can be challenging to solve, but with the right approach, you can master them. In this post, we will explore the steps to solve radical equations and provide tips to make the process easier.
Types of Radical Equations
There are two main types of radical equations: simple radical equations and complex radical equations. Simple radical equations involve only one radical expression, while complex radical equations involve multiple radical expressions.
- Simple radical equations: \sqrt{x} = 5
- Complex radical equations: \sqrt{x} + \sqrt{y} = 7
Step-by-Step Guide to Solving Radical Equations
Step 1: Isolate the Radical Expression
To solve a radical equation, start by isolating the radical expression on one side of the equation. This will make it easier to eliminate the radical.
Example: \sqrt{x} + 2 = 9
- Subtract 2 from both sides: \sqrt{x} = 7
Step 2: Eliminate the Radical
To eliminate the radical, raise both sides of the equation to the power of the radical. For example, if the radical is a square root, raise both sides to the power of 2.
Example: \sqrt{x} = 7
- Square both sides: x = 49
Step 3: Check the Solution
Once you have eliminated the radical, check the solution to make sure it is valid. Plug the solution back into the original equation to ensure that it is true.
Example: \sqrt{x} = 7
- Plug in x = 49: \sqrt{49} = 7 (True)
📝 Note: When checking the solution, make sure to plug the value back into the original equation, not the simplified equation.
Step 4: Solve for the Variable
If the solution is valid, solve for the variable. In this case, we already have the value of x.
Example: x = 49
Tips and Tricks for Solving Radical Equations
- Simplify the equation: Before solving the equation, simplify it as much as possible. This will make it easier to isolate the radical expression.
- Use inverse operations: To eliminate the radical, use inverse operations. For example, if the radical is a square root, use the square operation to eliminate it.
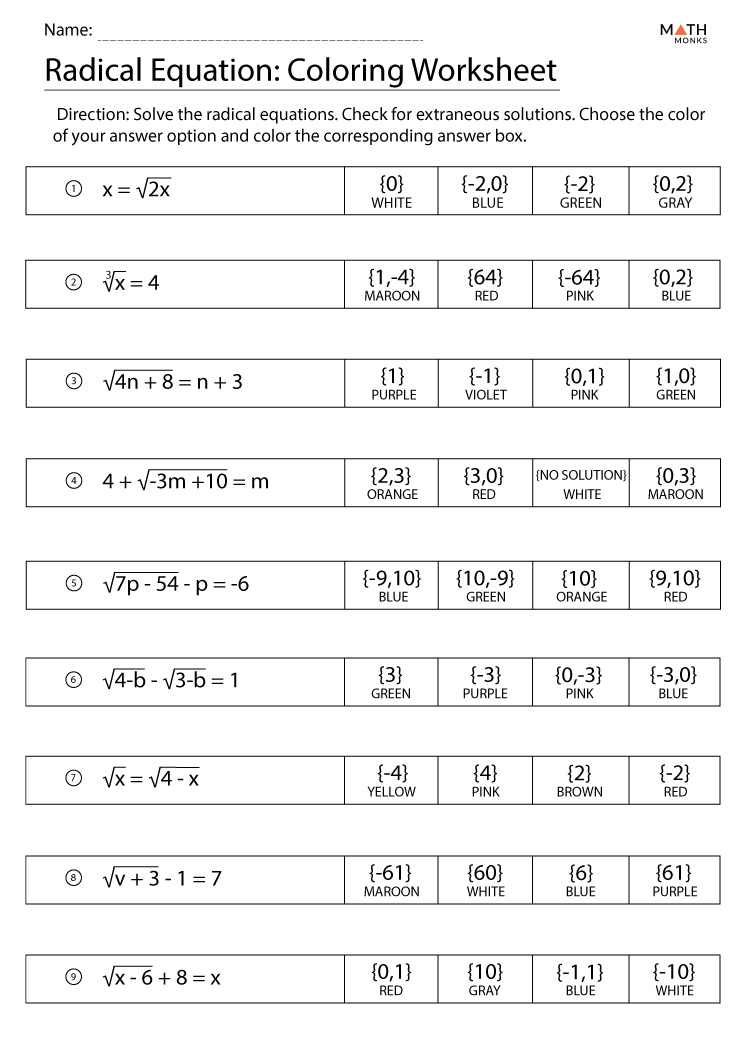
- Check for extraneous solutions: When solving radical equations, it’s possible to introduce extraneous solutions. Always check the solution to make sure it is valid.
| Radical Equation | Solution |
|---|---|
| $\sqrt{x} = 5$ | $x = 25$ |
| $\sqrt{x} + 2 = 9$ | $x = 49$ |
| $\sqrt{x} - 3 = 4$ | $x = 49$ |
Common Mistakes to Avoid
- Forgetting to check the solution: Always check the solution to make sure it is valid. This will help you avoid extraneous solutions.
- Using the wrong operation: To eliminate the radical, use the inverse operation. For example, if the radical is a square root, use the square operation.
- Not simplifying the equation: Simplify the equation as much as possible before solving it. This will make it easier to isolate the radical expression.
By following these steps and tips, you can easily solve radical equations. Remember to always check your solution and simplify the equation before solving it.
Solving radical equations requires patience and attention to detail. With practice, you can master these equations and become proficient in solving them.
What is a radical equation?
+A radical equation is an equation that contains a radical expression, which involves the square root or other roots of a number.
How do I eliminate the radical in a radical equation?
+To eliminate the radical, raise both sides of the equation to the power of the radical. For example, if the radical is a square root, raise both sides to the power of 2.
What is the importance of checking the solution in a radical equation?
+Checking the solution is important to ensure that it is valid and not an extraneous solution. Plug the solution back into the original equation to verify its validity.