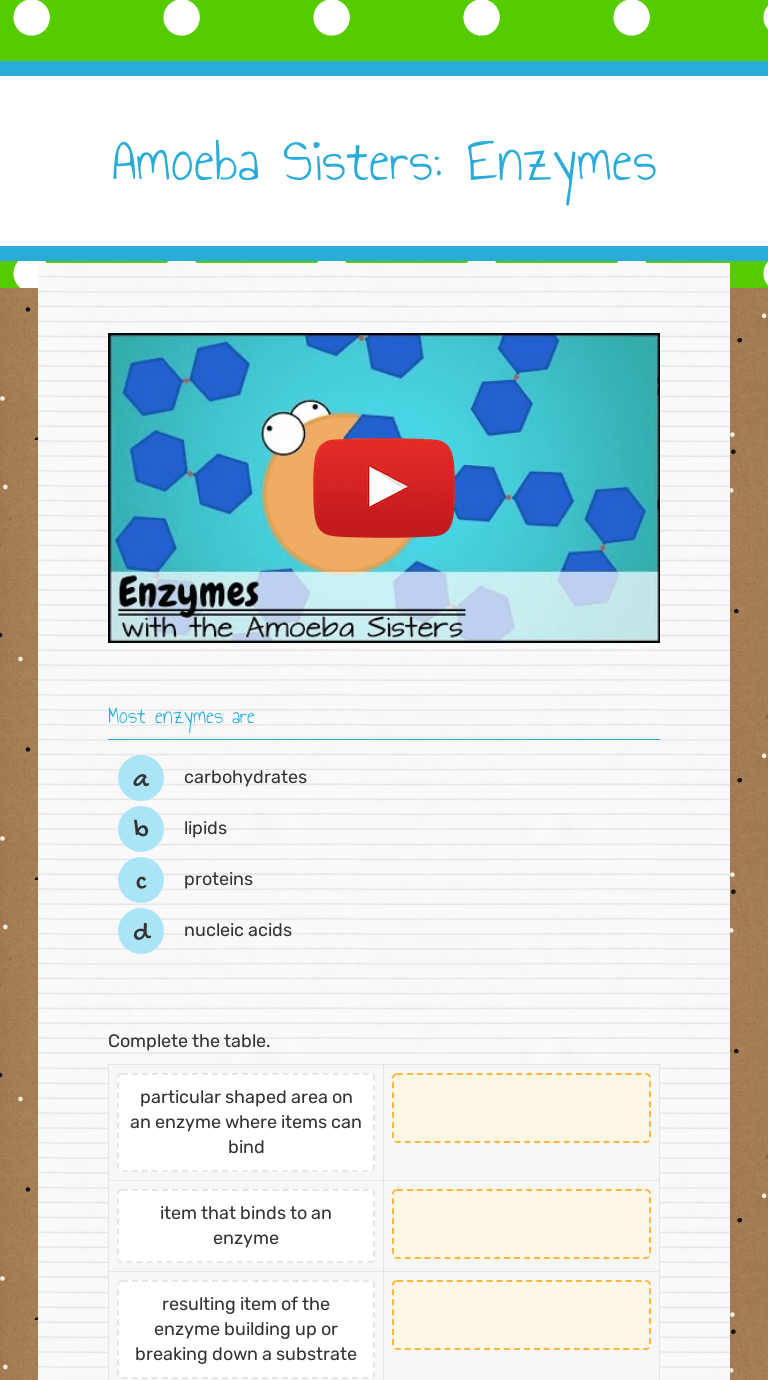
Solving Quadratic Equations By Graphing Worksheet
Understanding Quadratic Equations and Graphing
Quadratic equations are a fundamental concept in algebra, and graphing is a powerful tool for solving them. A quadratic equation is a polynomial equation of degree two, which means the highest power of the variable (usually x) is two. The general form of a quadratic equation is ax^2 + bx + c = 0, where a, b, and c are constants.
In this article, we will explore how to solve quadratic equations by graphing. We will discuss the basics of graphing quadratic equations, the benefits of this method, and provide a step-by-step guide on how to do it.
Why Graphing is an Effective Method for Solving Quadratic Equations
Graphing is an effective method for solving quadratic equations because it allows us to visualize the equation and its solutions. By graphing the equation, we can see the x-intercepts, which represent the solutions to the equation. This method is particularly useful when the equation cannot be factored easily or when we need to find the approximate solutions.
How to Graph a Quadratic Equation
To graph a quadratic equation, we need to follow these steps:
- Write the equation in the general form ax^2 + bx + c = 0.
- Determine the x-intercepts by factoring the equation or using the quadratic formula.
- Determine the vertex of the parabola by using the formula x = -b/2a.
- Plot the vertex and the x-intercepts on the coordinate plane.
- Draw a smooth curve through the points to create the graph.
📝 Note: If you're having trouble finding the x-intercepts or vertex, try using a graphing calculator or online tool to help you visualize the graph.
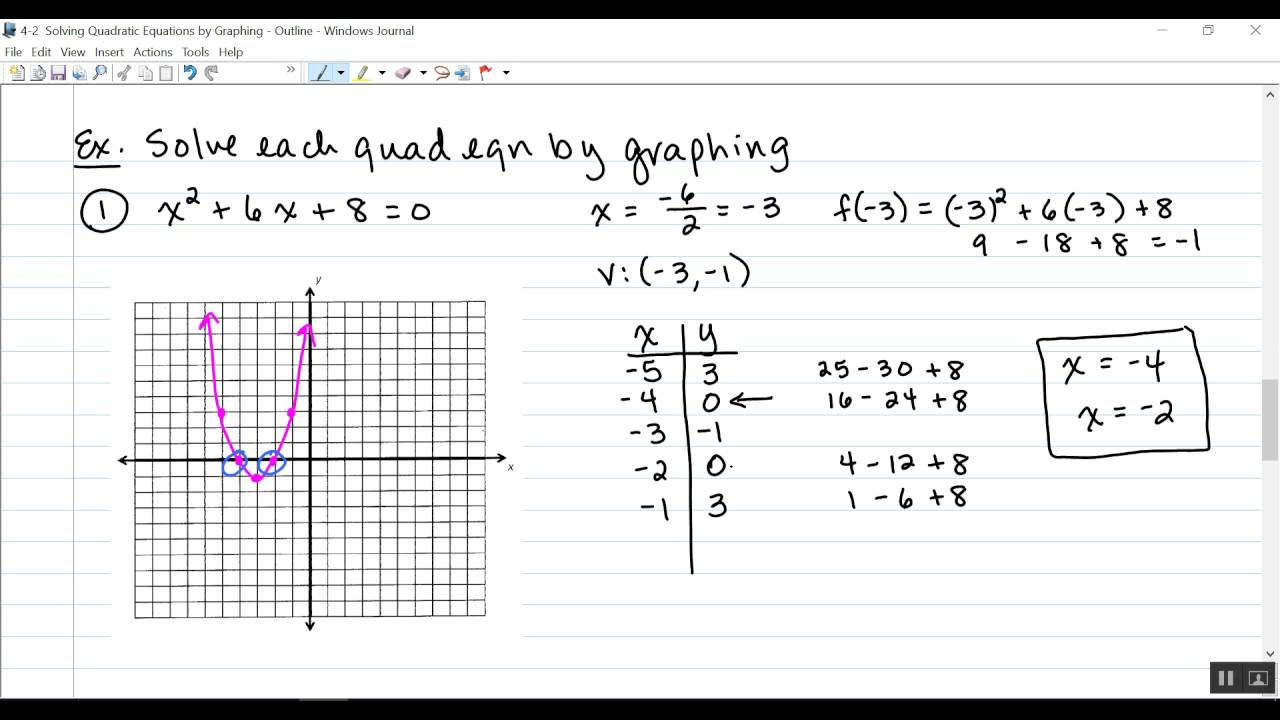
Step-by-Step Example: Graphing a Quadratic Equation
Let’s use the quadratic equation x^2 + 5x + 6 = 0 as an example.
- Write the equation in the general form: x^2 + 5x + 6 = 0.
- Determine the x-intercepts by factoring: (x + 3)(x + 2) = 0.
- Determine the vertex of the parabola: x = -5⁄2(1) = -5⁄2.
- Plot the vertex and the x-intercepts on the coordinate plane:

| x | y |
|---|---|
| -3 | 0 |
| -2 | 0 |
| -5⁄2 | 19⁄4 |
- Draw a smooth curve through the points to create the graph:
Graph:
The graph shows the x-intercepts at (-3, 0) and (-2, 0), and the vertex at (-5⁄2, 19⁄4).
Benefits of Graphing Quadratic Equations
Graphing quadratic equations has several benefits, including:
- Visual representation: Graphing allows us to visualize the equation and its solutions, making it easier to understand the relationship between the variables.
- Approximate solutions: Graphing can help us find approximate solutions to the equation, especially when the equation cannot be factored easily.
- Multiple solutions: Graphing can help us identify multiple solutions to the equation, which may not be apparent when using other methods.
Common Challenges and Solutions
When graphing quadratic equations, you may encounter some common challenges, such as:
- Difficulty finding x-intercepts: If you’re having trouble finding the x-intercepts, try using the quadratic formula or a graphing calculator to help you visualize the graph.
- Difficulty drawing the graph: If you’re having trouble drawing the graph, try using a graphing calculator or online tool to help you create a smooth curve.
📝 Note: If you're still having trouble, try breaking down the problem into smaller steps or seeking help from a teacher or tutor.
In conclusion, graphing is a powerful tool for solving quadratic equations. By following the steps outlined in this article, you can graph quadratic equations and find their solutions. Remember to use graphing calculators or online tools to help you visualize the graph, especially when faced with challenges.
What is the general form of a quadratic equation?
+
The general form of a quadratic equation is ax^2 + bx + c = 0, where a, b, and c are constants.
How do I determine the x-intercepts of a quadratic equation?
+
You can determine the x-intercepts by factoring the equation or using the quadratic formula.
What is the benefit of graphing quadratic equations?
+
Graphing quadratic equations allows us to visualize the equation and its solutions, making it easier to understand the relationship between the variables.
Related Terms:
- Problem solving quadratic equations Worksheet
- Quadratic graph worksheet
- Solve quadratic equation by graphing