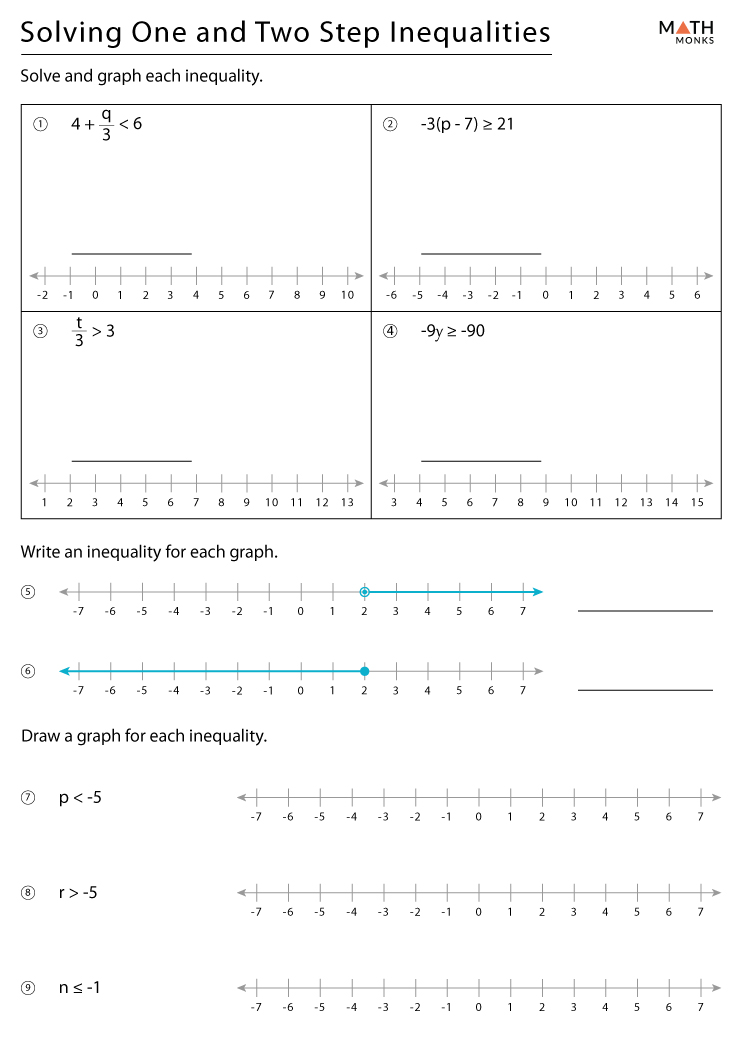
6 Ways to Solve Inequalities with Ease
Introduction to Inequalities
Inequalities are a fundamental concept in mathematics, used to compare the magnitude of two or more values. Solving inequalities is a crucial skill, as it allows us to determine the range of values that satisfy a given condition. In this article, we will explore six ways to solve inequalities with ease, covering various techniques and methods to help you master this topic.
Method 1: Add or Subtract the Same Value
One of the simplest ways to solve inequalities is to add or subtract the same value from both sides of the inequality. This method is based on the concept of equivalence, which states that if two expressions are equal, then adding or subtracting the same value from both expressions will not change the equality.
For example, consider the inequality:
2x + 3 > 5
To solve this inequality, we can subtract 3 from both sides:
2x > 2
Next, we can divide both sides by 2:
x > 1
This method is useful for solving simple inequalities, but it may not be sufficient for more complex cases.
📝 Note: When adding or subtracting the same value from both sides, make sure to perform the operation on both sides of the inequality to maintain the equality.
Method 2: Multiply or Divide by a Positive Value
Another way to solve inequalities is to multiply or divide both sides by a positive value. This method is based on the concept of equivalence, which states that if two expressions are equal, then multiplying or dividing both expressions by the same positive value will not change the equality.
For example, consider the inequality:
4x < 12
To solve this inequality, we can divide both sides by 4:
x < 3
This method is useful for solving inequalities that involve multiplication or division by a positive value.
📝 Note: When multiplying or dividing both sides by a positive value, make sure to perform the operation on both sides of the inequality to maintain the equality.
Method 3: Use the Multiplication Property of Inequality
The multiplication property of inequality states that if two expressions are equal, then multiplying both expressions by the same value will not change the equality. However, if the value is negative, the direction of the inequality will change.
For example, consider the inequality:
-3x > 9
To solve this inequality, we can multiply both sides by -1, but we need to change the direction of the inequality:
3x < -9
Next, we can divide both sides by 3:
x < -3
This method is useful for solving inequalities that involve multiplication by a negative value.
📝 Note: When multiplying both sides by a negative value, make sure to change the direction of the inequality to maintain the equality.
Method 4: Use the Division Property of Inequality
The division property of inequality states that if two expressions are equal, then dividing both expressions by the same value will not change the equality. However, if the value is negative, the direction of the inequality will change.
For example, consider the inequality:
-2x < 6
To solve this inequality, we can divide both sides by -2, but we need to change the direction of the inequality:
x > -3
This method is useful for solving inequalities that involve division by a negative value.
📝 Note: When dividing both sides by a negative value, make sure to change the direction of the inequality to maintain the equality.
Method 5: Use the Quadratic Formula
The quadratic formula is a powerful tool for solving quadratic inequalities. The formula is:
x = (-b ± √(b^2 - 4ac)) / 2a
For example, consider the inequality:
x^2 + 4x + 4 > 0
To solve this inequality, we can factor the left-hand side:
(x + 2)^2 > 0
This inequality is true for all values of x, since the square of any real number is always non-negative.
Method 6: Use Graphing
Graphing is a visual method for solving inequalities. By graphing the related function, we can determine the range of values that satisfy the inequality.
For example, consider the inequality:
x^2 - 4x - 3 > 0
To solve this inequality, we can graph the related function:
f(x) = x^2 - 4x - 3
By analyzing the graph, we can determine the range of values that satisfy the inequality.

| Method | Description |
|---|---|
| Add or Subtract the Same Value | Add or subtract the same value from both sides of the inequality. |
| Multiply or Divide by a Positive Value | Multiply or divide both sides of the inequality by a positive value. |
| Use the Multiplication Property of Inequality | Multiply both sides of the inequality by the same value, changing the direction of the inequality if the value is negative. |
| Use the Division Property of Inequality | Divide both sides of the inequality by the same value, changing the direction of the inequality if the value is negative. |
| Use the Quadratic Formula | Use the quadratic formula to solve quadratic inequalities. |
| Use Graphing | Graph the related function to determine the range of values that satisfy the inequality. |
In conclusion, solving inequalities is a crucial skill in mathematics, and there are several methods to achieve this. By mastering these six methods, you will be able to solve a wide range of inequalities with ease.
What is the difference between an equation and an inequality?
+An equation is a statement that expresses the equality of two mathematical expressions, whereas an inequality is a statement that expresses the non-equality of two mathematical expressions.
How do I determine the direction of the inequality when multiplying or dividing both sides by a negative value?
+When multiplying or dividing both sides of an inequality by a negative value, the direction of the inequality changes. For example, if you multiply both sides by -2, the inequality symbol will change from ‘>’ to ‘<’ or vice versa.
What is the quadratic formula, and how do I use it to solve inequalities?
+The quadratic formula is a mathematical formula that provides the solutions to a quadratic equation. To use the quadratic formula to solve inequalities, you need to factor the quadratic expression and then use the formula to find the solutions.
Related Terms:
- One Step Inequalities Worksheet PDF
- two-step inequalities worksheet 7th grade
- Solving Inequalities Worksheet PDF