5 Ways to Master Slope in Math
Understanding Slope in Math: A Comprehensive Guide
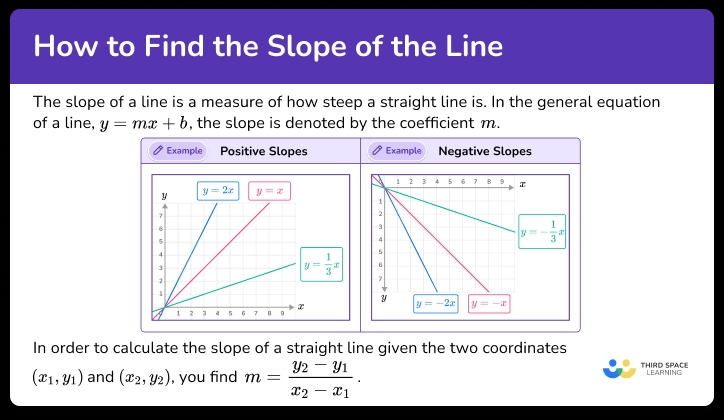
Slope is a fundamental concept in mathematics, particularly in algebra and geometry. It is a measure of how steep a line is and can be positive, negative, or zero. Mastering slope is crucial for solving various mathematical problems, including graphing lines, finding equations of lines, and determining the steepness of a line. In this article, we will explore five ways to master slope in math.
1. Definition and Formula
To start, it is essential to understand the definition and formula of slope. Slope is defined as the ratio of the vertical change (rise) to the horizontal change (run) between two points on a line. The formula for slope is:
m = (y2 - y1) / (x2 - x1)
where m is the slope, (x1, y1) and (x2, y2) are two points on the line.
📝 Note: The slope formula can be remembered using the phrase "rise over run."
2. Graphing Lines
Graphing lines is an excellent way to visualize slope. To graph a line, you need to know the slope and one point on the line. Using the slope formula, you can find the equation of the line in the form y = mx + b, where m is the slope and b is the y-intercept.
Here are the steps to graph a line:
- Plot the point on the graph.
- Use the slope to determine the direction and steepness of the line.
- Draw the line through the point, using the slope to guide you.
3. Finding Equations of Lines
Finding the equation of a line is a crucial skill in math. To find the equation of a line, you need to know the slope and one point on the line. Using the slope formula, you can find the equation of the line in the form y = mx + b.
Here are the steps to find the equation of a line:
- Find the slope using the formula m = (y2 - y1) / (x2 - x1).
- Use the slope and one point to find the equation of the line in the form y = mx + b.
4. Identifying Slope from a Graph
Identifying slope from a graph is an essential skill in math. To identify the slope from a graph, you need to find the ratio of the vertical change (rise) to the horizontal change (run) between two points on the line.
Here are the steps to identify slope from a graph:
- Find two points on the line.
- Measure the vertical change (rise) and horizontal change (run) between the two points.
- Use the slope formula to find the slope.
5. Real-World Applications
Slope has many real-world applications, including physics, engineering, and architecture. Understanding slope is essential for designing roads, bridges, and buildings.
Here are some examples of real-world applications of slope:
- Designing roads: Slope is used to determine the steepness of roads and highways.
- Building design: Slope is used to determine the steepness of roofs and stairs.
- Physics: Slope is used to determine the velocity and acceleration of objects.
What is the slope formula?
+The slope formula is m = (y2 - y1) / (x2 - x1).
How do I graph a line?
+To graph a line, plot the point on the graph, use the slope to determine the direction and steepness of the line, and draw the line through the point.
What are some real-world applications of slope?
+Slope has many real-world applications, including designing roads, building design, and physics.
In summary, mastering slope in math requires understanding the definition and formula, graphing lines, finding equations of lines, identifying slope from a graph, and understanding real-world applications. By following these steps and practicing regularly, you can become proficient in slope and improve your overall math skills.
Related Terms:
- Slope Worksheet PDF
- Slope worksheets 8th grade PDF
- Slope-intercept form worksheet