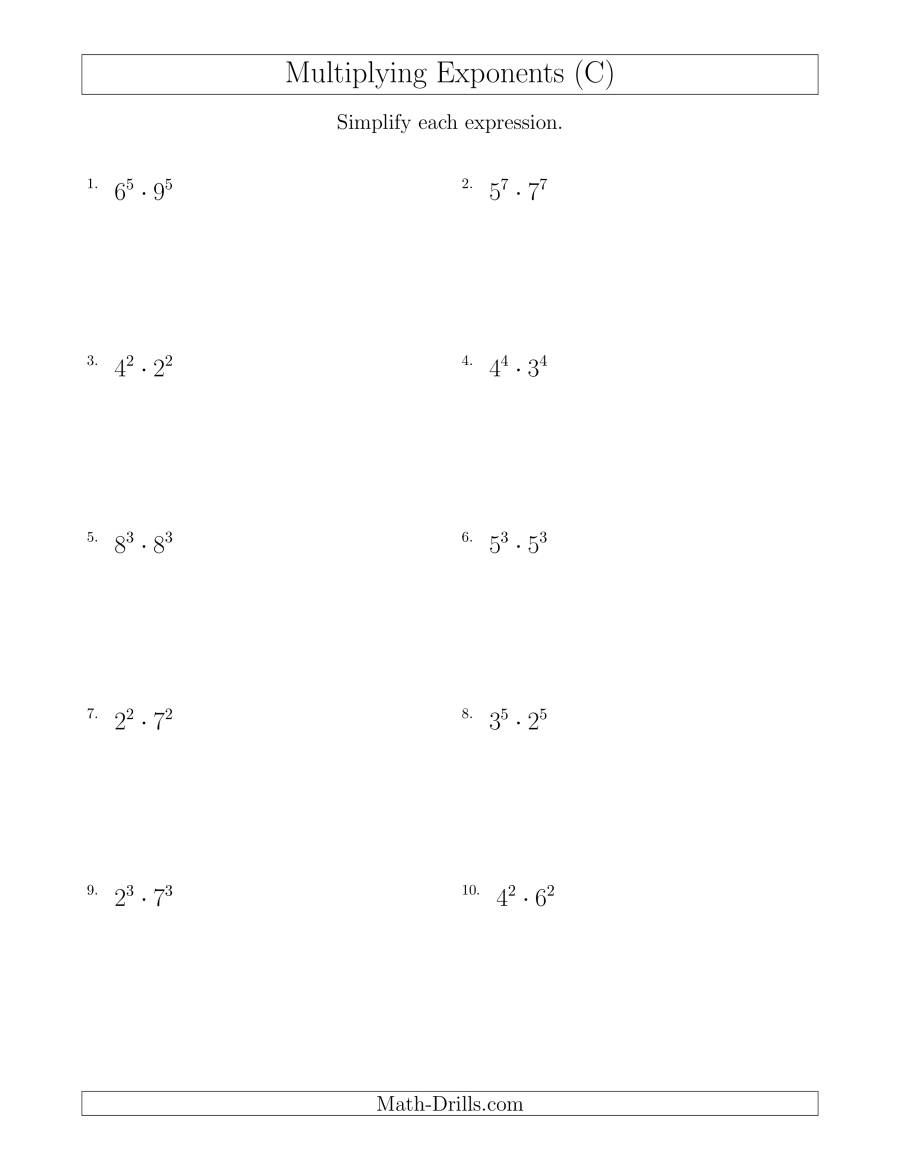
Understanding Exponents and Simplifying Expressions
Exponents are shorthand notation for repeated multiplication of the same number. They are used to simplify expressions and make calculations easier. In this article, we will explore how to simplify expressions using exponents and provide a worksheet to practice.
What are Exponents?
Exponents are numbers that are raised to a power. They are written in the form of a base number raised to a power, such as 2^3 or 5^2. The base number is the number being multiplied, and the power is the number of times it is multiplied.
For example, 2^3 is equal to 2 multiplied by itself three times: 2 × 2 × 2 = 8. Similarly, 5^2 is equal to 5 multiplied by itself two times: 5 × 5 = 25.
Laws of Exponents
There are several laws of exponents that help us simplify expressions. These laws are:
- Product of Powers Law: When multiplying two numbers with the same base, add the exponents. For example, 2^3 × 2^4 = 2^(3+4) = 2^7
- Power of a Power Law: When raising a number to a power and then raising that result to another power, multiply the exponents. For example, (2^3)^4 = 2^(3×4) = 2^12
- Power of a Product Law: When raising a product to a power, raise each factor to that power. For example, (2 × 3)^4 = 2^4 × 3^4
Simplifying Expressions with Exponents
Using the laws of exponents, we can simplify expressions by combining like terms and applying the laws.
For example, simplify the expression: 2^3 × 2^2
Using the Product of Powers Law, we add the exponents: 2^3 × 2^2 = 2^(3+2) = 2^5
Similarly, simplify the expression: (3^2)^3
Using the Power of a Power Law, we multiply the exponents: (3^2)^3 = 3^(2×3) = 3^6
Worksheet: Simplifying Expressions with Exponents
Here is a worksheet to practice simplifying expressions with exponents:
| Expression | Simplified Expression |
|---|---|
| 2^3 × 2^2 | ______ |
| (3^2)^3 | ______ |
| 5^2 × 5^4 | ______ |
| (2 × 3)^4 | ______ |
| 4^3 × 4^2 | ______ |
💡 Note: Use the laws of exponents to simplify each expression.
Answer Key
| Expression | Simplified Expression |
|---|---|
| 2^3 × 2^2 | 2^5 |
| (3^2)^3 | 3^6 |
| 5^2 × 5^4 | 5^6 |
| (2 × 3)^4 | 2^4 × 3^4 |
| 4^3 × 4^2 | 4^5 |
Conclusion
Exponents are a powerful tool for simplifying expressions and making calculations easier. By understanding the laws of exponents and practicing with worksheets, you can become proficient in simplifying expressions with exponents.
What is an exponent?
+An exponent is a number that is raised to a power. It is written in the form of a base number raised to a power, such as 2^3 or 5^2.
What is the Product of Powers Law?
+The Product of Powers Law states that when multiplying two numbers with the same base, add the exponents. For example, 2^3 × 2^4 = 2^(3+4) = 2^7.
How do I simplify expressions with exponents?
+To simplify expressions with exponents, use the laws of exponents to combine like terms and apply the laws. For example, simplify the expression: 2^3 × 2^2 by adding the exponents: 2^3 × 2^2 = 2^(3+2) = 2^5.
