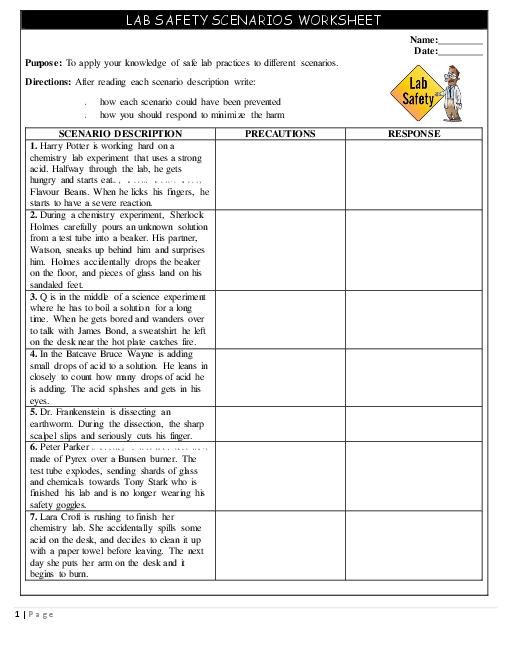
Same Perimeter Different Area Math Worksheets

Understanding Same Perimeter Different Area Math Concept
In mathematics, the concept of perimeter and area is essential in understanding the properties of various shapes. While the perimeter of a shape refers to the total length of its boundary, the area represents the amount of space inside the shape. Interestingly, it is possible to have shapes with the same perimeter but different areas. This concept is crucial in various mathematical applications, including geometry, architecture, and design.
What is Perimeter?
The perimeter of a shape is the total distance around its boundary. It is calculated by adding up the lengths of all the sides of the shape. For example, the perimeter of a rectangle is calculated by adding the lengths of all its sides, which is equivalent to 2 times the length plus 2 times the width (2l + 2w).
What is Area?
The area of a shape is the amount of space inside the shape. It is measured in square units, such as square centimeters or square meters. The area of a rectangle, for instance, is calculated by multiplying its length and width (l x w).
Same Perimeter Different Area Concept
Now, let’s explore the concept of same perimeter different area. This concept implies that two or more shapes can have the same perimeter but different areas. This is possible because the perimeter only depends on the length of the sides, whereas the area depends on the arrangement of the sides.
Examples of Same Perimeter Different Area
Here are a few examples to illustrate this concept:
- A rectangle with a length of 6 units and a width of 4 units has a perimeter of 20 units (2l + 2w = 2(6) + 2(4) = 20). Its area is 24 square units (l x w = 6 x 4 = 24).
- A square with a side length of 5 units has a perimeter of 20 units (4s = 4(5) = 20). Its area is 25 square units (s x s = 5 x 5 = 25).
- A triangle with two sides of 6 units and 8 units, and a third side of 10 units, has a perimeter of 24 units (a + b + c = 6 + 8 + 10 = 24). Its area is 12 square units (using the formula for the area of a triangle).
Math Worksheets for Same Perimeter Different Area
To help students understand this concept, here are some math worksheets that you can use:
Worksheet 1:
Find the perimeter and area of each shape:
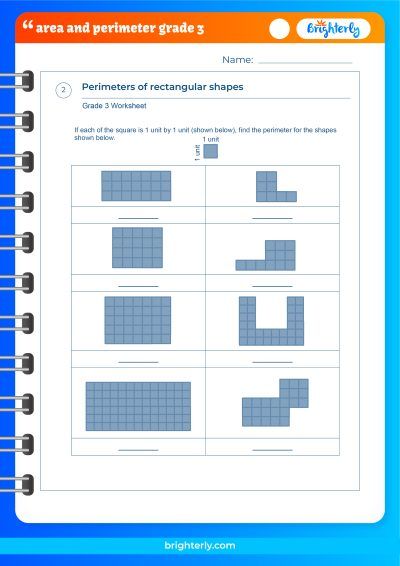
| Shape | Length | Width | Perimeter | Area |
|---|---|---|---|---|
| Rectangle | 5 | 3 | ||
| Square | 4 | |||
| Triangle | 6 | 8 |
Worksheet 2:
Compare the perimeters and areas of the following shapes:
| Shape 1 | Shape 2 | Perimeter | Area |
|---|---|---|---|
| Rectangle (6 x 4) | Square (5) | ||
| Triangle (6, 8, 10) | Rectangle (5 x 3) |
Tips for Solving Same Perimeter Different Area Problems
When solving problems involving same perimeter different area, keep the following tips in mind:
- Read the problem carefully and identify the given information.
- Use the formulas for perimeter and area to calculate the values.
- Compare the perimeters and areas of the shapes to determine if they are the same or different.
Conclusion
In conclusion, the concept of same perimeter different area is an essential idea in mathematics that helps us understand the properties of various shapes. By using math worksheets and practicing problems, students can develop a deeper understanding of this concept and apply it to real-world situations.
FAQ
What is the perimeter of a shape?
+
The perimeter of a shape is the total distance around its boundary.
Can two shapes have the same perimeter but different areas?
+
Yes, two shapes can have the same perimeter but different areas.
How can I calculate the area of a shape?
+
The area of a shape can be calculated using various formulas, such as length x width for rectangles or the formula for the area of a triangle.
Related Terms:
- Area and perimeter worksheets
- Mixed area and Perimeter worksheets