7 Ways to Master Rational vs Irrational Numbers
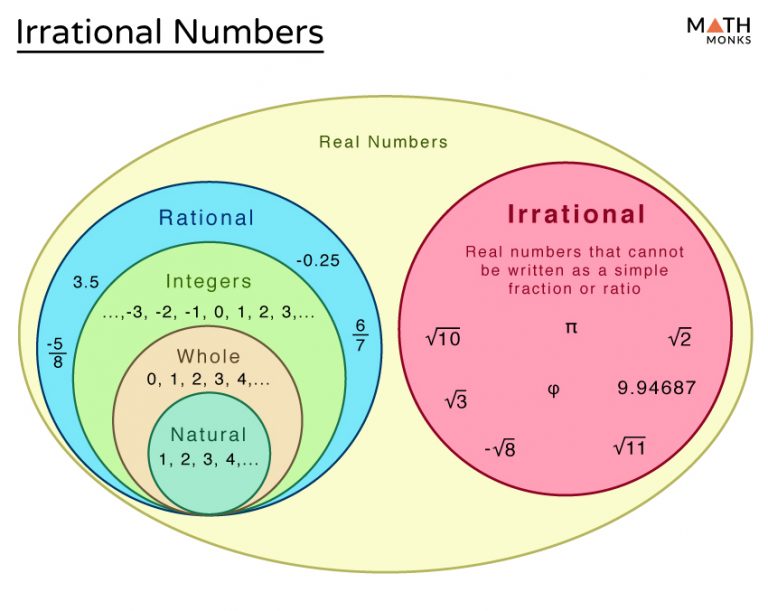
Understanding Rational and Irrational Numbers
Rational and irrational numbers are two fundamental concepts in mathematics that can be confusing, especially for students who are new to these terms. In this article, we will delve into the world of rational and irrational numbers, exploring their definitions, differences, and practical applications. We will also provide 7 ways to master these concepts, making it easier for you to understand and work with them.
What are Rational Numbers?
Rational numbers are numbers that can be expressed as the ratio of two integers, i.e., a fraction. In other words, a rational number is a number that can be written in the form of a/b, where a and b are integers and b is non-zero. Examples of rational numbers include:
- 3⁄4
- 22⁄7
- 1⁄2
Rational numbers can be further divided into two subcategories:
- Integers: These are rational numbers that can be expressed as a ratio of two integers, where the denominator is 1. Examples of integers include -3, 0, and 5.
- Fractions: These are rational numbers that can be expressed as a ratio of two integers, where the denominator is not 1. Examples of fractions include 3⁄4 and 2⁄3.
What are Irrational Numbers?
Irrational numbers, on the other hand, are numbers that cannot be expressed as a ratio of two integers. In other words, an irrational number is a number that cannot be written in the form of a/b, where a and b are integers and b is non-zero. Examples of irrational numbers include:
- π (pi)
- e (Euler’s number)
- √2 (the square root of 2)
Irrational numbers are often encountered in geometry and trigonometry, particularly when dealing with circles and triangles.
Key Differences between Rational and Irrational Numbers
Here are some key differences between rational and irrational numbers:
- Expressibility: Rational numbers can be expressed as a ratio of two integers, while irrational numbers cannot.
- Terminability: Rational numbers have a finite number of digits, while irrational numbers have an infinite number of digits that never repeat in a predictable pattern.
- Operations: Rational numbers can be added, subtracted, multiplied, and divided using standard arithmetic operations, while irrational numbers require more advanced mathematical operations, such as algebraic manipulation.
7 Ways to Master Rational and Irrational Numbers
Mastering rational and irrational numbers requires practice, patience, and a deep understanding of mathematical concepts. Here are 7 ways to help you master these concepts:
- Understand the definitions: Make sure you understand the definitions of rational and irrational numbers, including their properties and characteristics.
- Practice converting between forms: Practice converting rational numbers between their fraction and decimal forms, and vice versa.
- Learn to identify rational and irrational numbers: Practice identifying whether a given number is rational or irrational, and explain your reasoning.
- Use real-world examples: Use real-world examples to illustrate the practical applications of rational and irrational numbers, such as in finance, science, and engineering.
- Work with algebraic expressions: Work with algebraic expressions that involve rational and irrational numbers, such as solving equations and manipulating formulas.
- Visualize mathematical concepts: Use visual aids, such as graphs and charts, to help you understand and visualize mathematical concepts, such as the distribution of rational and irrational numbers on the number line.
- Apply mathematical concepts to problem-solving: Apply mathematical concepts, such as rational and irrational numbers, to problem-solving in various contexts, such as physics, engineering, and computer science.
📝 Note: Mastering rational and irrational numbers requires a deep understanding of mathematical concepts, as well as practice and patience. Start by reviewing the definitions and properties of these numbers, and then practice working with them in different contexts.
Common Applications of Rational and Irrational Numbers
Rational and irrational numbers have numerous applications in various fields, including:
- Finance: Rational numbers are used in finance to calculate interest rates, investment returns, and currency exchange rates.
- Science: Irrational numbers are used in science to describe the properties of physical systems, such as the circumference of a circle (π) and the square root of 2 (√2).
- Engineering: Rational and irrational numbers are used in engineering to design and optimize systems, such as bridges, buildings, and electronic circuits.
- Computer Science: Rational and irrational numbers are used in computer science to develop algorithms and data structures, such as binary search trees and hash tables.
Conclusion
Rational and irrational numbers are fundamental concepts in mathematics that have numerous applications in various fields. By understanding the definitions, properties, and practical applications of these numbers, you can develop a deeper appreciation for the beauty and complexity of mathematics. With practice and patience, you can master rational and irrational numbers and apply them to solve problems in various contexts.
What is the difference between a rational and an irrational number?
+A rational number is a number that can be expressed as the ratio of two integers, while an irrational number is a number that cannot be expressed as a ratio of two integers.
Can a rational number be expressed as a decimal?
+Yes, a rational number can be expressed as a decimal, but it will have a finite number of digits or repeat in a predictable pattern.
What is an example of an irrational number?
+An example of an irrational number is π (pi), which is approximately equal to 3.14159 but has an infinite number of digits that never repeat in a predictable pattern.