5 Ways to Master Quadratic Regression
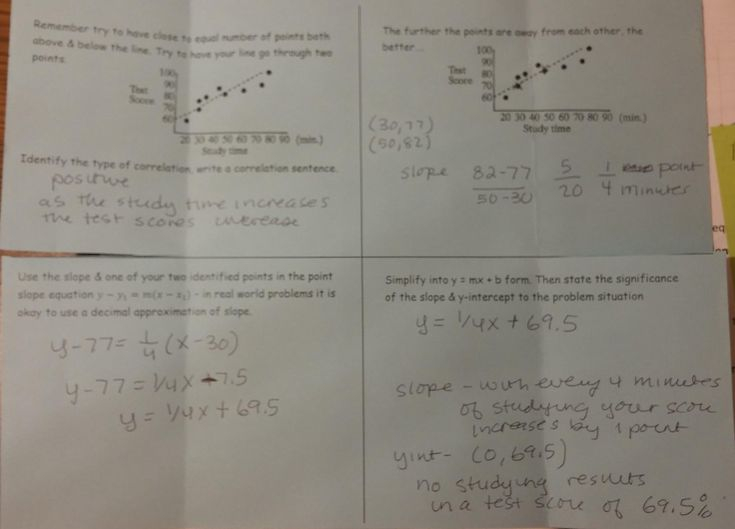
Understanding Quadratic Regression
Quadratic regression is a statistical technique used to model the relationship between a dependent variable and one or more independent variables. It is a type of nonlinear regression analysis that is used to predict the value of a continuous outcome variable based on one or more predictor variables. In this blog post, we will explore five ways to master quadratic regression, including understanding the basics, selecting the right model, interpreting results, avoiding common pitfalls, and using quadratic regression in practice.
1. Understanding the Basics of Quadratic Regression
Quadratic regression is a type of regression analysis that uses a quadratic equation to model the relationship between a dependent variable and one or more independent variables. The quadratic equation takes the form of:
Y = β0 + β1X + β2X^2 + ε
Where:
- Y is the dependent variable
- X is the independent variable
- β0, β1, and β2 are the regression coefficients
- ε is the error term
Quadratic regression is used to model relationships that are not linear, but rather curved or parabolic. It is commonly used in fields such as economics, finance, and engineering to model complex relationships between variables.
📝 Note: Quadratic regression is a powerful tool for modeling nonlinear relationships, but it can be sensitive to outliers and non-normality in the data.
2. Selecting the Right Model for Quadratic Regression
When selecting a model for quadratic regression, there are several factors to consider. These include:
- Model specification: The model should be specified in a way that captures the underlying relationship between the variables.
- Variable selection: The variables included in the model should be relevant and meaningful.
- Model complexity: The model should be complex enough to capture the underlying relationship, but not so complex that it becomes difficult to interpret.
Some common models used for quadratic regression include:
- Polynomial regression: This model uses a quadratic equation to model the relationship between the variables.
- Piecewise regression: This model uses a combination of linear and quadratic equations to model the relationship between the variables.
- Generalized additive models: This model uses a combination of linear and nonlinear terms to model the relationship between the variables.
Table: Comparison of Quadratic Regression Models
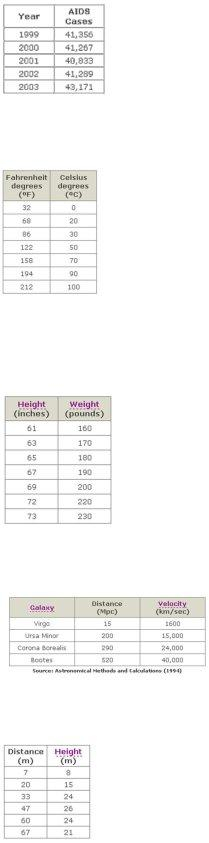
| Model | Description | Advantages | Disadvantages |
|---|---|---|---|
| Polynomial regression | Uses a quadratic equation to model the relationship between variables | Easy to interpret, can capture complex relationships | Can be sensitive to outliers and non-normality |
| Piecewise regression | Uses a combination of linear and quadratic equations to model the relationship between variables | Can capture complex relationships, robust to outliers | Can be difficult to interpret, requires careful selection of breakpoints |
| Generalized additive models | Uses a combination of linear and nonlinear terms to model the relationship between variables | Can capture complex relationships, robust to outliers | Can be difficult to interpret, requires careful selection of terms |
3. Interpreting Results from Quadratic Regression
Interpreting the results from quadratic regression requires careful consideration of the coefficients, standard errors, and p-values. The coefficients represent the change in the dependent variable for a one-unit change in the independent variable, while the standard errors represent the uncertainty in the estimates. The p-values represent the probability of observing the estimated relationship by chance.
Some common metrics used to evaluate the performance of quadratic regression models include:
- R-squared: Measures the proportion of variance in the dependent variable that is explained by the model.
- Mean squared error: Measures the average squared difference between the predicted and actual values of the dependent variable.
- Root mean squared error: Measures the square root of the mean squared error.
📊 Note: Quadratic regression models can be sensitive to outliers and non-normality in the data, which can affect the interpretation of the results.
4. Avoiding Common Pitfalls in Quadratic Regression
There are several common pitfalls to avoid when using quadratic regression, including:
- Overfitting: Occurs when the model is too complex and captures random noise in the data.
- Underfitting: Occurs when the model is too simple and fails to capture the underlying relationship between the variables.
- Multicollinearity: Occurs when two or more independent variables are highly correlated, which can affect the estimates of the regression coefficients.
To avoid these pitfalls, it is essential to:
- Use cross-validation: Split the data into training and testing sets to evaluate the performance of the model.
- Use regularization techniques: Use techniques such as ridge regression or lasso regression to reduce the impact of multicollinearity.
- Use diagnostic plots: Use plots such as residual plots and normal probability plots to diagnose potential issues with the model.
5. Using Quadratic Regression in Practice
Quadratic regression has a wide range of applications in fields such as economics, finance, and engineering. Some common examples of using quadratic regression in practice include:
- Predicting stock prices: Quadratic regression can be used to model the relationship between stock prices and economic indicators such as GDP and inflation.
- Modeling energy consumption: Quadratic regression can be used to model the relationship between energy consumption and temperature.
- Predicting sports outcomes: Quadratic regression can be used to model the relationship between sports outcomes and team performance metrics such as points scored and yards gained.
By following these five steps, you can master quadratic regression and apply it to a wide range of problems in practice.
Practical Applications of Quadratic Regression
Quadratic regression has a wide range of practical applications in fields such as economics, finance, and engineering. Some common examples of using quadratic regression in practice include:
- Predicting stock prices: Quadratic regression can be used to model the relationship between stock prices and economic indicators such as GDP and inflation.
- Modeling energy consumption: Quadratic regression can be used to model the relationship between energy consumption and temperature.
- Predicting sports outcomes: Quadratic regression can be used to model the relationship between sports outcomes and team performance metrics such as points scored and yards gained.
Quadratic regression can also be used to model complex relationships between variables in fields such as:
- Economics: Quadratic regression can be used to model the relationship between economic indicators such as GDP and inflation.
- Finance: Quadratic regression can be used to model the relationship between stock prices and economic indicators such as GDP and inflation.
- Engineering: Quadratic regression can be used to model the relationship between physical systems and variables such as temperature and pressure.
By applying quadratic regression to these fields, you can gain a deeper understanding of the complex relationships between variables and make more accurate predictions.
Quadratic regression is a powerful tool for modeling nonlinear relationships between variables. By understanding the basics of quadratic regression, selecting the right model, interpreting results, avoiding common pitfalls, and using quadratic regression in practice, you can master this technique and apply it to a wide range of problems in practice.
In conclusion, mastering quadratic regression requires a combination of theoretical knowledge and practical experience. By following the five steps outlined in this blog post, you can develop a deep understanding of quadratic regression and apply it to a wide range of problems in practice. Whether you are a student, researcher, or practitioner, quadratic regression is a valuable tool to have in your toolkit.
What is quadratic regression?
+Quadratic regression is a statistical technique used to model the relationship between a dependent variable and one or more independent variables. It is a type of nonlinear regression analysis that is used to predict the value of a continuous outcome variable based on one or more predictor variables.
What are some common applications of quadratic regression?
+Quadratic regression has a wide range of applications in fields such as economics, finance, and engineering. Some common examples of using quadratic regression in practice include predicting stock prices, modeling energy consumption, and predicting sports outcomes.
How do I avoid common pitfalls in quadratic regression?
+To avoid common pitfalls in quadratic regression, it is essential to use cross-validation, use regularization techniques, and use diagnostic plots. You should also be aware of the potential for overfitting, underfitting, and multicollinearity.
Related Terms:
- Quadratic regression worksheet
- Quadratic regression Worksheet PDF
- Quadratic regression calculator
- Linear and quadratic regression Worksheet



