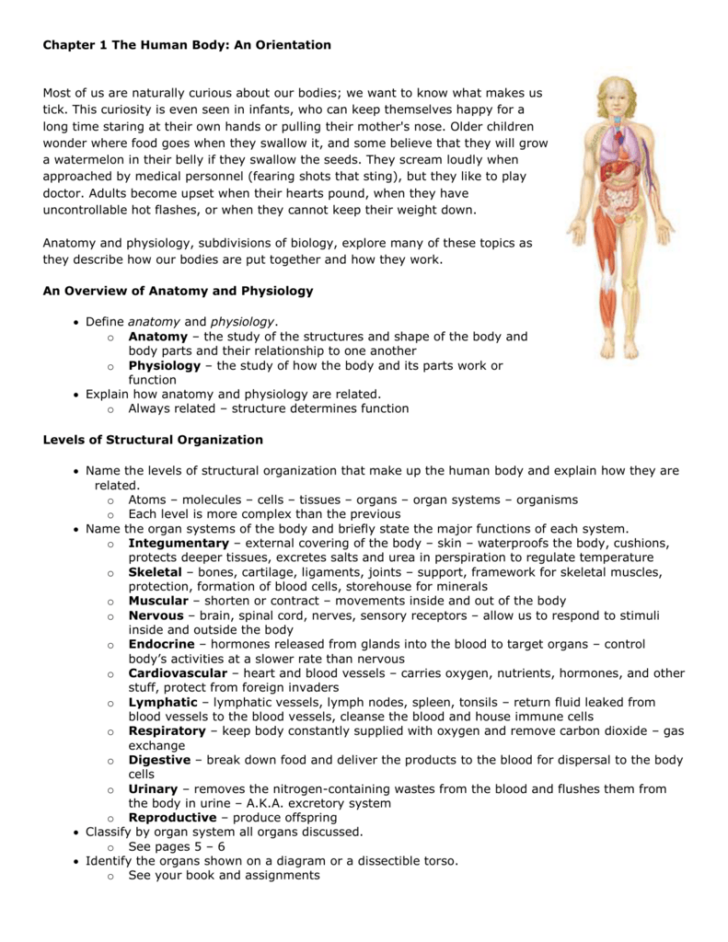
Pythagorean Theorem Converse Problems and Solutions

Understanding the Pythagorean Theorem Converse

The Pythagorean Theorem is a fundamental concept in geometry that describes the relationship between the lengths of the sides of a right-angled triangle. The converse of the Pythagorean Theorem is also an essential concept that can help us determine whether a triangle is right-angled or not. In this blog post, we will explore the Pythagorean Theorem converse, provide examples of problems and solutions, and offer important notes and a FAQ section.

What is the Pythagorean Theorem Converse?

The Pythagorean Theorem converse states that if the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides, then the triangle is right-angled. Mathematically, this can be expressed as:

c² = a² + b²

where c is the length of the hypotenuse, and a and b are the lengths of the other two sides.

Example Problems and Solutions

Let’s consider a few examples to illustrate the Pythagorean Theorem converse.

Example 1:

In a triangle, the length of the hypotenuse is 10 cm, and the lengths of the other two sides are 6 cm and 8 cm. Is the triangle right-angled?

Solution:

Using the Pythagorean Theorem converse, we can calculate:

c² = 10² = 100 a² + b² = 6² + 8² = 36 + 64 = 100

Since c² = a² + b², the triangle is right-angled.

Example 2:

In a triangle, the lengths of the sides are 5 cm, 12 cm, and 13 cm. Is the triangle right-angled?

Solution:

Using the Pythagorean Theorem converse, we can calculate:

c² = 13² = 169 a² + b² = 5² + 12² = 25 + 144 = 169

Since c² = a² + b², the triangle is right-angled.

Example 3:

In a triangle, the lengths of the sides are 8 cm, 15 cm, and 17 cm. Is the triangle right-angled?

Solution:

Using the Pythagorean Theorem converse, we can calculate:

c² = 17² = 289 a² + b² = 8² + 15² = 64 + 225 = 289

Since c² = a² + b², the triangle is right-angled.

Important Notes

📝 Note: The Pythagorean Theorem converse is a necessary and sufficient condition for a triangle to be right-angled. This means that if the theorem is true, the triangle is right-angled, and if the triangle is right-angled, the theorem is true.

📝 Note: The Pythagorean Theorem converse can be used to determine whether a triangle is right-angled, but it cannot be used to determine whether a triangle is obtuse or acute.

Conclusion

In this blog post, we have explored the Pythagorean Theorem converse and provided examples of problems and solutions. We have also highlighted important notes and a FAQ section. The Pythagorean Theorem converse is a powerful tool for determining whether a triangle is right-angled, and it has many practical applications in geometry and trigonometry.