Pythagorean Theorem And Its Converse Worksheet

Understanding the Pythagorean Theorem and Its Converse
The Pythagorean Theorem is a fundamental concept in geometry, used to calculate the length of the hypotenuse of a right-angled triangle. The theorem states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. This can be expressed mathematically as:
a² + b² = c²
where a and b are the lengths of the two sides that form the right angle, and c is the length of the hypotenuse.
Applying the Pythagorean Theorem
To apply the Pythagorean Theorem, you need to know the lengths of two sides of a right-angled triangle. Then, you can use the formula to calculate the length of the third side.
For example, let’s say you have a right-angled triangle with one side that is 3 inches long, and the other side that is 4 inches long. To calculate the length of the hypotenuse, you would use the formula like this:
3² + 4² = c² 9 + 16 = c² 25 = c² c = √25 c = 5 inches
Therefore, the length of the hypotenuse is 5 inches.
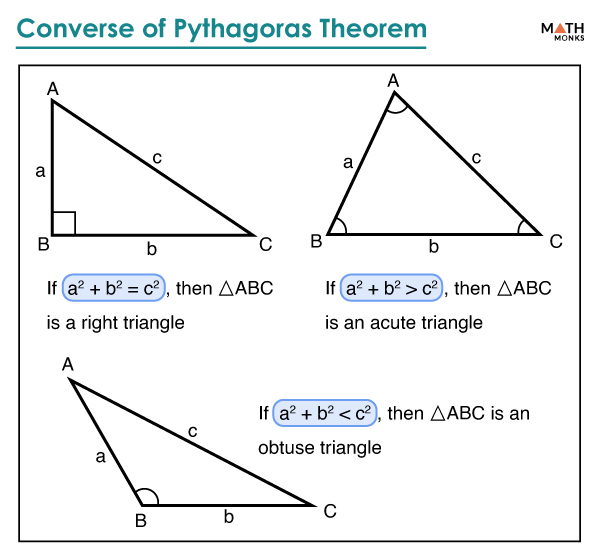
The Converse of the Pythagorean Theorem
The converse of the Pythagorean Theorem is a related concept that can be used to determine whether a triangle is a right-angled triangle or not. The converse states that if the square of the length of the longest side of a triangle is equal to the sum of the squares of the lengths of the other two sides, then the triangle is a right-angled triangle.
Mathematically, this can be expressed as:
c² = a² + b²
If this equation is true, then the triangle is a right-angled triangle.
Worksheet
Now, let’s practice applying the Pythagorean Theorem and its converse with some exercises.
Exercise 1
In a right-angled triangle, one side is 5 cm long, and the other side is 12 cm long. Calculate the length of the hypotenuse.
| Side 1 | Side 2 | Hypotenuse |
|---|---|---|
| 5 cm | 12 cm | ? |
Exercise 2
A triangle has sides of length 8 cm, 15 cm, and 17 cm. Is this a right-angled triangle? Use the converse of the Pythagorean Theorem to determine.
| Side 1 | Side 2 | Side 3 | Right-angled? |
|---|---|---|---|
| 8 cm | 15 cm | 17 cm | ? |
Exercise 3
In a right-angled triangle, the length of the hypotenuse is 10 inches, and one of the other sides is 6 inches long. Calculate the length of the third side.
| Hypotenuse | Side 1 | Side 2 |
|---|---|---|
| 10 inches | 6 inches | ? |
Exercise 4
A triangle has sides of length 9 cm, 12 cm, and 15 cm. Is this a right-angled triangle? Use the converse of the Pythagorean Theorem to determine.
| Side 1 | Side 2 | Side 3 | Right-angled? |
|---|---|---|---|
| 9 cm | 12 cm | 15 cm | ? |
📝 Note: You can use a calculator to help you with the calculations.
Solutions
Exercise 1
5² + 12² = c² 25 + 144 = c² 169 = c² c = √169 c = 13 cm
Therefore, the length of the hypotenuse is 13 cm.
Exercise 2
17² = 8² + 15² 289 = 64 + 225 289 = 289
Since the equation is true, this is a right-angled triangle.
Exercise 3
10² = 6² + b² 100 = 36 + b² b² = 64 b = √64 b = 8 inches
Therefore, the length of the third side is 8 inches.
Exercise 4
15² = 9² + 12² 225 = 81 + 144 225 = 225
Since the equation is true, this is a right-angled triangle.
To summarize, the Pythagorean Theorem is a powerful tool for calculating the length of the hypotenuse of a right-angled triangle, while its converse can be used to determine whether a triangle is right-angled or not. By practicing with exercises like these, you can become more confident in applying these concepts to solve problems.
What is the Pythagorean Theorem?
+The Pythagorean Theorem is a mathematical concept that states that in a right-angled triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides.
What is the converse of the Pythagorean Theorem?
+The converse of the Pythagorean Theorem states that if the square of the length of the longest side of a triangle is equal to the sum of the squares of the lengths of the other two sides, then the triangle is a right-angled triangle.
How do I apply the Pythagorean Theorem?
+To apply the Pythagorean Theorem, you need to know the lengths of two sides of a right-angled triangle. Then, you can use the formula to calculate the length of the third side.
Related Terms:
- Converse of the Pythagorean Theorem
- Pythagorean Theorem Worksheet PDF
- Pythagorean Theorem PDF