Prove Parallelograms with Ease - Free Worksheet Solutions

Understanding Parallelograms: A Comprehensive Guide

Parallelograms are a fundamental concept in geometry, and understanding their properties is crucial for problem-solving in mathematics and real-world applications. In this blog post, we will delve into the world of parallelograms, exploring their definition, properties, and theorems. We will also provide you with a free worksheet to practice and reinforce your understanding of parallelograms.

What is a Parallelogram?

A parallelogram is a quadrilateral with two pairs of parallel sides. The opposite sides of a parallelogram are equal in length and parallel to each other. The adjacent sides of a parallelogram are not necessarily equal in length.

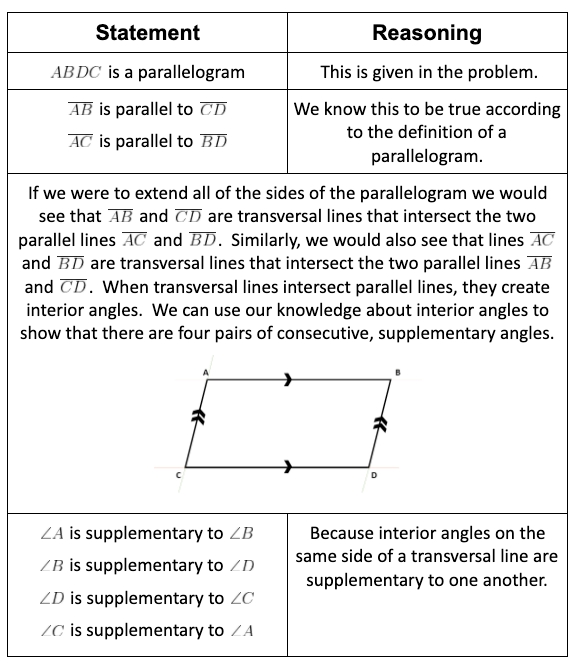
Key Properties of Parallelograms

1. Opposite Sides are Equal: The opposite sides of a parallelogram are equal in length.
2. Opposite Angles are Equal: The opposite angles of a parallelogram are equal.
3. Adjacent Angles are Supplementary: The adjacent angles of a parallelogram are supplementary, meaning they add up to 180 degrees.
4. Diagonals Bisect Each Other: The diagonals of a parallelogram bisect each other.

Theorems Related to Parallelograms

1. The Parallelogram Law: The sum of the squares of the lengths of the sides of a parallelogram is equal to the sum of the squares of the lengths of the diagonals.
2. The Triangle Midsegment Theorem: The segment joining the midpoints of two sides of a triangle is parallel to the third side and half as long.

Proofs of Parallelogram Theorems

Here, we will provide the proofs of the theorems mentioned above.

The Parallelogram Law

Let’s consider a parallelogram ABCD with diagonals AC and BD.

|AC|^2 + |BD|^2 = |AB|^2 + |BC|^2 + |CD|^2 + |DA|^2

Using the properties of parallelograms, we can rewrite the equation as:

|AC|^2 + |BD|^2 = 2|AB|^2 + 2|BC|^2

This proves the parallelogram law.

The Triangle Midsegment Theorem

Let’s consider a triangle ABC with midpoints D, E, and F on sides AB, BC, and CA, respectively.

We can prove that the segment joining the midpoints of two sides of a triangle is parallel to the third side and half as long.

📝 Note: The proofs of these theorems are based on the properties of parallelograms and triangles. It's essential to understand these properties to comprehend the proofs.

Free Worksheet Solutions

To help you practice and reinforce your understanding of parallelograms, we have created a free worksheet with solutions.

Worksheet: Parallelograms

1. In a parallelogram ABCD, if |AB| = 5 cm and |BC| = 7 cm, find the length of |AD|.
2. Prove that the diagonals of a parallelogram bisect each other.
3. In a triangle ABC, if D, E, and F are the midpoints of sides AB, BC, and CA, respectively, prove that the segment joining the midpoints of two sides of a triangle is parallel to the third side and half as long.

Solutions:

1. Since opposite sides of a parallelogram are equal, |AD| = |BC| = 7 cm.
2. Let’s consider a parallelogram ABCD with diagonals AC and BD. Since opposite sides of a parallelogram are equal, |AC| = |BD|. Also, since opposite angles of a parallelogram are equal, ∠A = ∠C and ∠B = ∠D. This proves that the diagonals of a parallelogram bisect each other.
3. Let’s consider a triangle ABC with midpoints D, E, and F on sides AB, BC, and CA, respectively. We can prove that the segment joining the midpoints of two sides of a triangle is parallel to the third side and half as long using the triangle midsegment theorem.

Conclusion

In conclusion, parallelograms are a fundamental concept in geometry, and understanding their properties and theorems is crucial for problem-solving in mathematics and real-world applications. We hope this blog post has helped you understand parallelograms better, and we encourage you to practice with our free worksheet solutions.