6 Ways to Master Proportional vs Non Proportional
Understanding the Basics of Proportional and Non-Proportional Relationships
When dealing with mathematical relationships, it’s essential to understand the concepts of proportional and non-proportional relationships. These relationships are fundamental in various fields, including physics, engineering, economics, and more. In this article, we’ll explore the differences between proportional and non-proportional relationships, and provide six ways to master these concepts.
What are Proportional Relationships?
Proportional relationships occur when a change in one variable causes a proportional change in another variable. In other words, as one variable increases or decreases, the other variable changes in a consistent and predictable manner. This type of relationship can be represented by the equation:
y = kx
where y is the dependent variable, x is the independent variable, and k is the constant of proportionality.
What are Non-Proportional Relationships?
Non-proportional relationships, on the other hand, occur when a change in one variable does not result in a proportional change in another variable. This type of relationship can be represented by more complex equations, such as quadratic or exponential equations.
6 Ways to Master Proportional vs Non-Proportional Relationships
1. Understand the Concept of Proportionality
To master proportional relationships, it’s essential to understand the concept of proportionality. Proportionality means that as one variable changes, the other variable changes in a consistent and predictable manner. This concept is crucial in various fields, including physics, engineering, and economics.
2. Identify Proportional Relationships in Real-Life Scenarios
To develop a deeper understanding of proportional relationships, try to identify them in real-life scenarios. For example, the cost of goods is often directly proportional to the quantity purchased. This means that if the quantity purchased increases, the cost will also increase in a consistent and predictable manner.
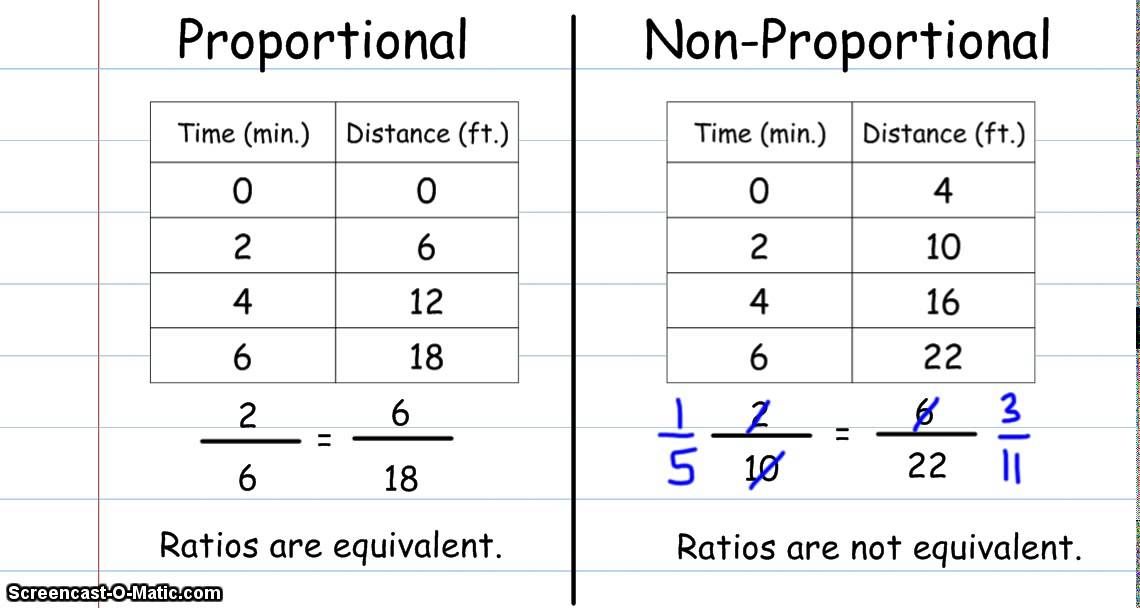
3. Use Graphs to Visualize Proportional Relationships
Graphs are an excellent way to visualize proportional relationships. By plotting the independent variable (x) against the dependent variable (y), you can see the relationship between the two variables. If the graph is a straight line, it indicates a proportional relationship.
4. Solve Problems Involving Proportional Relationships
To master proportional relationships, practice solving problems that involve these relationships. For example, if a bakery sells 200 loaves of bread at $2 each, how much will it sell 300 loaves of bread for? This type of problem requires you to understand the concept of proportionality and apply it to real-life scenarios.
5. Understand the Concept of Non-Proportionality
Non-proportional relationships are just as important as proportional relationships. To master non-proportional relationships, understand that they occur when a change in one variable does not result in a proportional change in another variable. This type of relationship can be represented by more complex equations, such as quadratic or exponential equations.
6. Practice Solving Problems Involving Non-Proportional Relationships
To develop a deeper understanding of non-proportional relationships, practice solving problems that involve these relationships. For example, if the temperature of a substance increases exponentially with time, how can you model this relationship using an equation?
📝 Note: When solving problems involving non-proportional relationships, it's essential to identify the type of relationship and choose the correct equation to model it.
Table: Examples of Proportional and Non-Proportional Relationships
| Type of Relationship | Example | Equation |
|---|---|---|
| Proportional | Cost of goods vs quantity purchased | y = kx |
| Non-Proportional | Temperature of a substance vs time | y = ab^x |
| Proportional | Distance traveled vs time | y = kx |
| Non-Proportional | Population growth vs time | y = ab^x |
In summary, mastering proportional and non-proportional relationships requires a deep understanding of the concepts and the ability to apply them to real-life scenarios. By following the six ways outlined in this article, you’ll be well on your way to developing a strong foundation in these fundamental concepts.
To recap, the key points to take away from this article are:
- Proportional relationships occur when a change in one variable causes a proportional change in another variable.
- Non-proportional relationships occur when a change in one variable does not result in a proportional change in another variable.
- Understanding the concept of proportionality and non-proportionality is crucial in various fields, including physics, engineering, and economics.
- Graphs can be used to visualize proportional relationships.
- Solving problems involving proportional and non-proportional relationships can help deepen your understanding of these concepts.
By applying these concepts to real-life scenarios and practicing solving problems, you’ll develop a strong foundation in proportional and non-proportional relationships.
What is the main difference between proportional and non-proportional relationships?
+The main difference between proportional and non-proportional relationships is that proportional relationships occur when a change in one variable causes a proportional change in another variable, while non-proportional relationships occur when a change in one variable does not result in a proportional change in another variable.
How can I identify proportional relationships in real-life scenarios?
+You can identify proportional relationships in real-life scenarios by looking for situations where a change in one variable causes a consistent and predictable change in another variable. For example, the cost of goods is often directly proportional to the quantity purchased.
What type of equation is used to model non-proportional relationships?
+Non-proportional relationships can be modeled using more complex equations, such as quadratic or exponential equations. For example, the temperature of a substance may increase exponentially with time, and this relationship can be modeled using an exponential equation.