5 Ways to Master Plotting Points on a Coordinate Plane
Understanding the Coordinate Plane
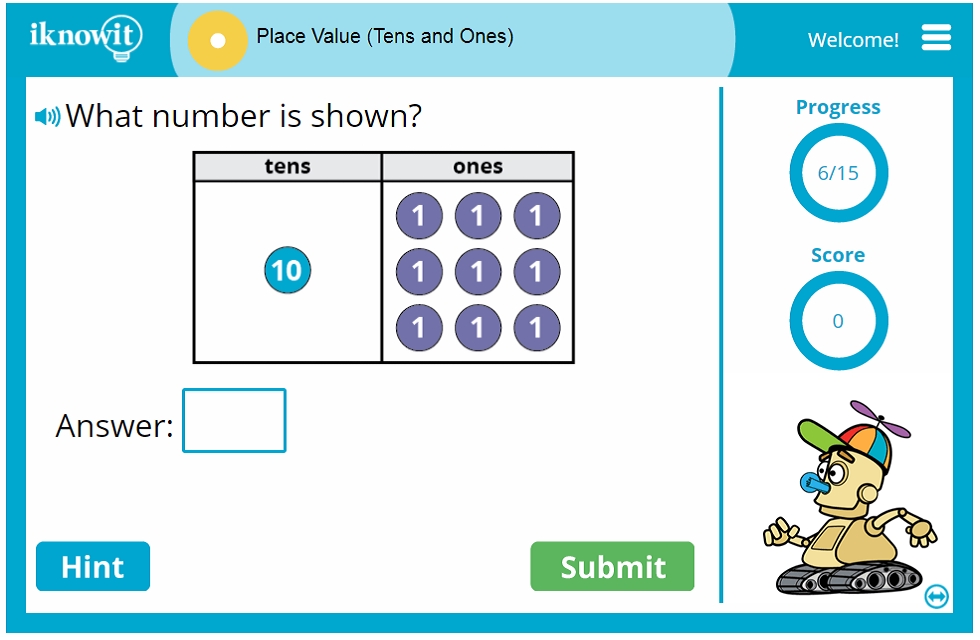
The coordinate plane is a fundamental concept in mathematics, used to visualize and graph relationships between two variables. It is a two-dimensional representation of points, where each point is defined by a unique set of coordinates (x, y). The x-coordinate represents the horizontal position, while the y-coordinate represents the vertical position. Mastering the art of plotting points on a coordinate plane is essential for various mathematical and real-world applications.
Recalling the Basics
Before diving into the methods, it is crucial to recall the basic structure of the coordinate plane:
- The x-axis represents the horizontal dimension, with positive values to the right and negative values to the left.
- The y-axis represents the vertical dimension, with positive values upwards and negative values downwards.
- The origin (0, 0) is the point where the x-axis and y-axis intersect.
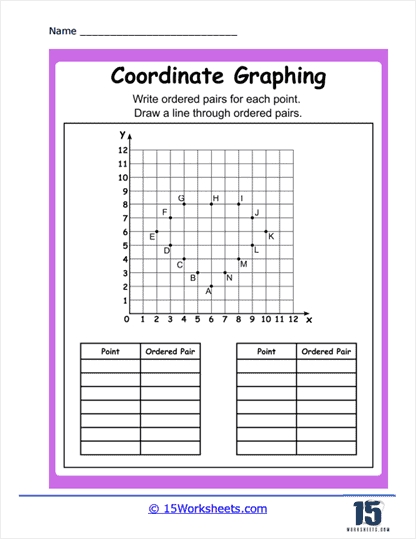
Method 1: Plotting Points using Coordinates
The most straightforward method of plotting points is by using their coordinates. To do this:
- Identify the x-coordinate and move horizontally to the corresponding point on the x-axis.
- From that point, move vertically to the corresponding y-coordinate.
- Mark the point where you stopped.
📍 Note: Make sure to label the point with its coordinates (x, y).
Method 2: Using a Graphing Calculator or Software
Graphing calculators and software can be used to plot points quickly and accurately. These tools allow you to enter the coordinates and visualize the points on the coordinate plane.
Some popular graphing calculators and software include:
- Desmos
- GeoGebra
- Graphing Calculator by Mathway
💻 Note: Familiarize yourself with the software's interface and settings to get the most out of it.
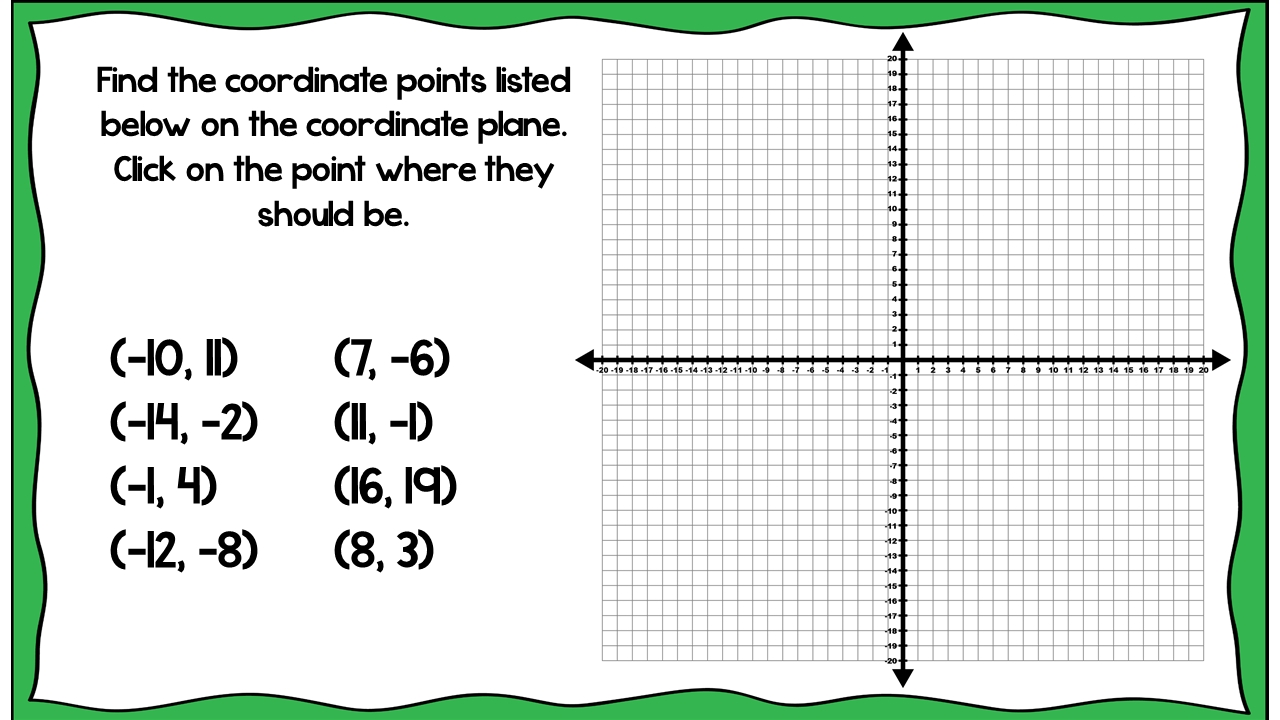
Method 3: Plotting Points from a Table of Values
When given a table of values, you can plot points by following these steps:
- Identify the x and y values for each point.
- Plot each point on the coordinate plane using the corresponding x and y values.
- Connect the points to form a line or curve, if applicable.
| x | y |
|---|---|
| 1 | 2 |
| 2 | 4 |
| 3 | 6 |
Method 4: Plotting Points from an Equation
Given an equation, you can plot points by substituting x values and solving for y.
For example, consider the equation y = 2x + 1:
- Substitute x = 1 and solve for y: y = 2(1) + 1 = 3
- Plot the point (1, 3) on the coordinate plane
- Repeat the process for different x values to plot more points
📝 Note: Make sure to label the points with their coordinates (x, y).
Method 5: Plotting Points using Patterns and Relationships
When dealing with patterns or relationships, you can plot points by identifying the underlying structure.
For example, consider the pattern of consecutive integers:
- Identify the starting point (x, y) = (1, 1)
- Move horizontally to the next integer and increment the y-coordinate by 1
- Repeat the process to plot more points
By mastering these five methods, you will become proficient in plotting points on a coordinate plane, a crucial skill for various mathematical and real-world applications.
In conclusion, plotting points on a coordinate plane is an essential skill that can be developed through practice and application of various methods. By understanding the basics of the coordinate plane and using the methods outlined above, you can improve your ability to visualize and graph relationships between variables.
What is the purpose of the coordinate plane?
+The coordinate plane is a two-dimensional representation of points, used to visualize and graph relationships between two variables.
How do I plot points from a table of values?
+Identify the x and y values for each point, and plot each point on the coordinate plane using the corresponding x and y values.
What is the difference between the x-axis and y-axis?
+The x-axis represents the horizontal dimension, with positive values to the right and negative values to the left. The y-axis represents the vertical dimension, with positive values upwards and negative values downwards.