6 Ways to Master Piecewise Functions

Understanding Piecewise Functions
Piecewise functions are a fundamental concept in mathematics, particularly in algebra and calculus. They are used to describe a function that has different expressions or formulas for different intervals or domains. In essence, a piecewise function is a way to combine multiple functions into one, where each function is defined for a specific interval or condition. Mastering piecewise functions is crucial for problem-solving in various fields, including physics, engineering, and economics.
What are Piecewise Functions?
A piecewise function is a function that is defined by multiple sub-functions, each applied to a specific interval or domain. The function is “pieced together” from these sub-functions, hence the name. Each sub-function is defined for a specific range of input values, and the function switches between these sub-functions as the input values change.
For example, consider the following piecewise function:
f(x) = { 2x, x < 0 { x^2, x ≥ 0
In this example, the function f(x) has two sub-functions: 2x for x < 0, and x^2 for x ≥ 0. The function switches between these two sub-functions at x = 0.
Why are Piecewise Functions Important?
Piecewise functions are essential in mathematics and science because they allow us to model complex phenomena that cannot be described by a single function. They are used to:
- Model real-world phenomena, such as the motion of objects, population growth, and electrical circuits
- Simplify complex problems by breaking them down into smaller, more manageable pieces
- Analyze and solve problems in calculus, differential equations, and linear algebra
6 Ways to Master Piecewise Functions
Mastering piecewise functions requires practice, patience, and a deep understanding of the underlying concepts. Here are six ways to help you master piecewise functions:
1. Understand the Domain and Range
The domain of a piecewise function is the set of all input values for which the function is defined. The range is the set of all possible output values. To master piecewise functions, you need to understand how to find the domain and range of each sub-function and how they relate to the overall function.
Example: Find the domain and range of the piecewise function:
f(x) = { x^2, x < 0 { 2x, x ≥ 0
The domain of the function is all real numbers, x ∈ (-∞, ∞). The range is all non-negative real numbers, y ∈ [0, ∞).
2. Identify the Sub-Functions
To work with piecewise functions, you need to identify the sub-functions that make up the overall function. This involves analyzing the function and identifying the different expressions or formulas that are used for different intervals or domains.
Example: Identify the sub-functions of the piecewise function:
f(x) = { x^2, x < 0 { 2x, x ≥ 0
The sub-functions are x^2 for x < 0 and 2x for x ≥ 0.
3. Graph the Sub-Functions
Graphing the sub-functions is an essential step in understanding piecewise functions. By graphing each sub-function, you can visualize how the function behaves for different intervals or domains.
Example: Graph the sub-functions of the piecewise function:
f(x) = { x^2, x < 0 { 2x, x ≥ 0
The graph of the sub-function x^2 for x < 0 is a parabola that opens upwards, while the graph of the sub-function 2x for x ≥ 0 is a straight line.
4. Evaluate the Function
Evaluating a piecewise function involves substituting a value of x into the function and determining which sub-function to use. This requires careful attention to the intervals or domains defined for each sub-function.
Example: Evaluate the piecewise function:
f(x) = { x^2, x < 0 { 2x, x ≥ 0
at x = -2.
Since x = -2 is less than 0, we use the sub-function x^2. Therefore, f(-2) = (-2)^2 = 4.
5. Simplify the Function
Simplifying a piecewise function involves combining like terms and eliminating any unnecessary complexity. This can help make the function easier to work with and understand.
Example: Simplify the piecewise function:
f(x) = { x^2 + 2x, x < 0 { 2x + 1, x ≥ 0
The simplified function is:
f(x) = { x(x + 2), x < 0 { 2x + 1, x ≥ 0
6. Practice, Practice, Practice
Finally, the key to mastering piecewise functions is practice. Work through many examples and exercises to develop your skills and confidence.
Example: Practice evaluating and simplifying piecewise functions with the following exercises:
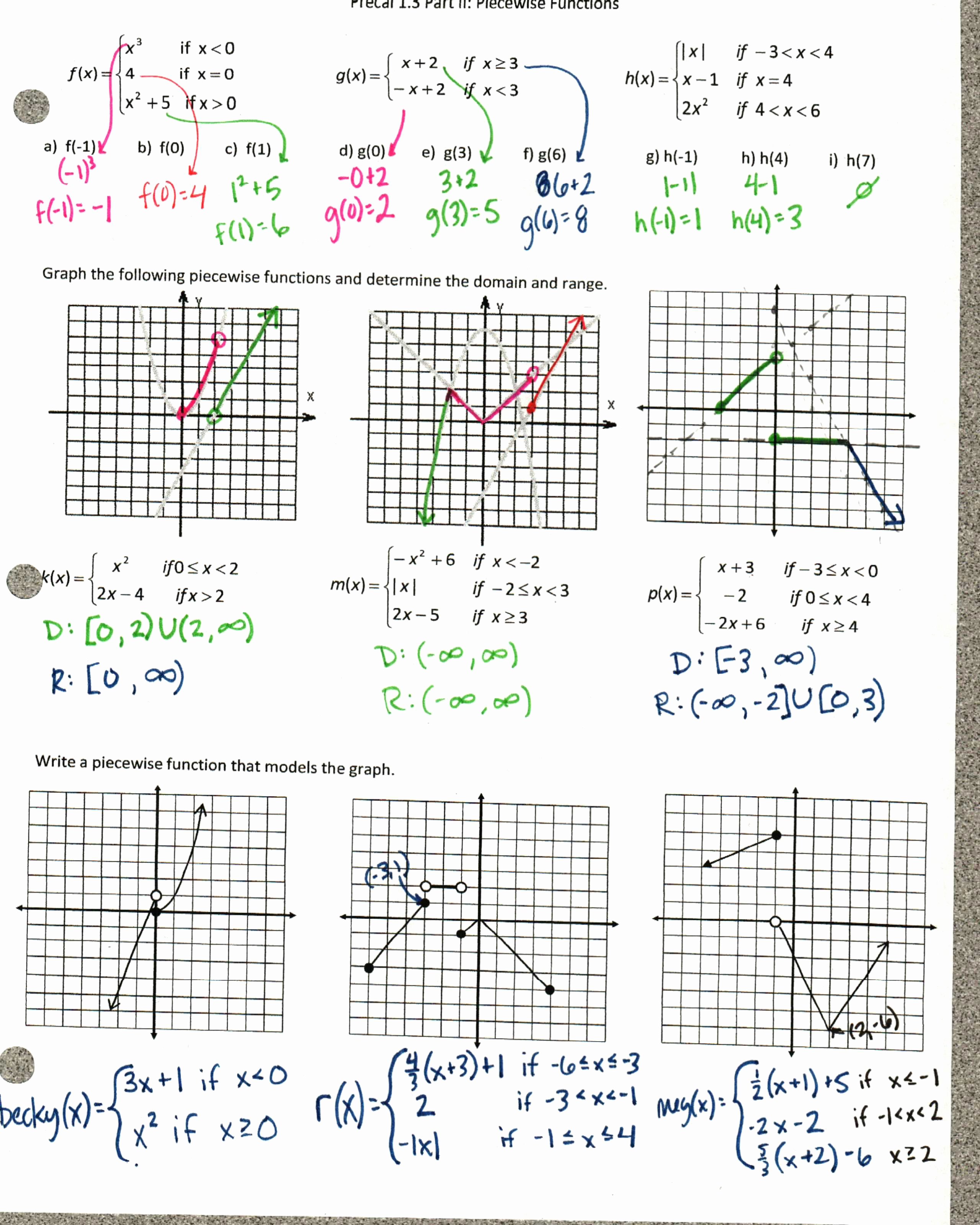
| Exercise | Function | Value of x |
|---|---|---|
| 1 | f(x) = { x^2, x < 0 | x = -3 |
| { 2x, x ≥ 0 | ||
| 2 | f(x) = { x + 1, x < 2 | x = 1 |
| { 2x - 1, x ≥ 2 |
Answers:
| Exercise | Answer |
|---|---|
| 1 | f(-3) = (-3)^2 = 9 |
| 2 | f(1) = 1 + 1 = 2 |
💡 Note: The exercises and examples provided are for illustration purposes only. You should practice with a variety of piecewise functions to develop your skills and confidence.
Conclusion
Mastering piecewise functions requires a deep understanding of the underlying concepts, as well as practice and patience. By following these six steps, you can develop the skills and confidence needed to work with piecewise functions. Remember to always identify the sub-functions, graph the sub-functions, evaluate the function, simplify the function, and practice, practice, practice!
What is a piecewise function?
+A piecewise function is a function that is defined by multiple sub-functions, each applied to a specific interval or domain.
Why are piecewise functions important?
+Piecewise functions are essential in mathematics and science because they allow us to model complex phenomena that cannot be described by a single function.
How do I evaluate a piecewise function?
+To evaluate a piecewise function, substitute a value of x into the function and determine which sub-function to use, based on the intervals or domains defined for each sub-function.
Related Terms:
- Graphing piecewise functions worksheet
- Piecewise Functions Worksheet pdf
- Evaluating piecewise Functions worksheet
- Algebra 2 piecewise Functions Worksheet