6 Ways to Master Parent Functions and Their Transformations

Understanding Parent Functions and Their Transformations

Parent functions are the basic building blocks of all functions in mathematics. They are the simplest form of a function, and all other functions can be derived from them through various transformations. Mastering parent functions and their transformations is essential for any student of mathematics, as it enables them to understand and work with more complex functions.

In this article, we will explore six ways to master parent functions and their transformations. We will discuss the different types of parent functions, their characteristics, and how to transform them. By the end of this article, you will have a deeper understanding of parent functions and be able to apply transformations to create more complex functions.

1. Identify the Parent Function

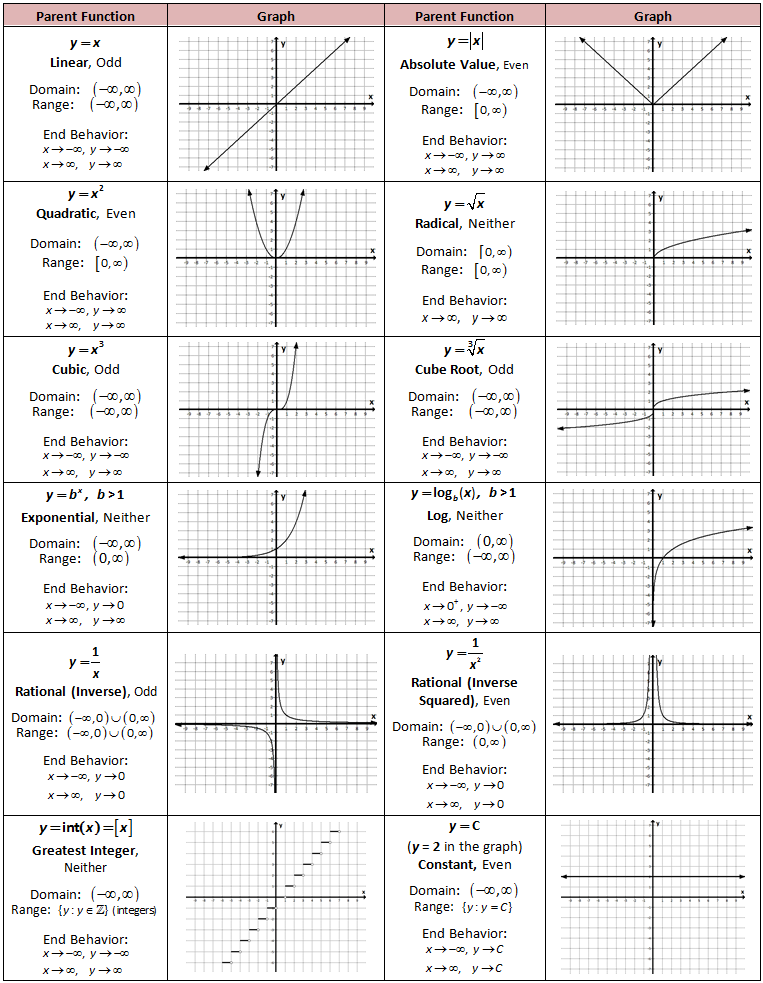
The first step in mastering parent functions is to be able to identify them. There are several types of parent functions, including:

• Linear functions: f(x) = x
• Quadratic functions: f(x) = x^2
• Cubic functions: f(x) = x^3
• Absolute value functions: f(x) = |x|
• Exponential functions: f(x) = 2^x
• Logarithmic functions: f(x) = log(x)

Each parent function has its own unique characteristics, such as its graph, domain, and range. Being able to identify the parent function is crucial in understanding how to transform it.

2. Understand the Transformations

Once you have identified the parent function, you need to understand how to transform it. There are several types of transformations, including:

• Vertical shifts: f(x) = f(x) + k
• Horizontal shifts: f(x) = f(x - h)
• Reflections: f(x) = -f(x)
• Stretches: f(x) = af(x)
• Compressions: f(x) = (1/a)f(x)

These transformations can be applied individually or in combination to create more complex functions.

3. Practice, Practice, Practice

Practice is key to mastering parent functions and their transformations. Start by practicing simple transformations, such as vertical and horizontal shifts. Gradually move on to more complex transformations, such as reflections and stretches.

Here are some examples of exercises you can try:

• Find the equation of the function that results from shifting the parent function f(x) = x^2 up 3 units.
• Find the equation of the function that results from reflecting the parent function f(x) = |x| across the x-axis.

4. Use Graphing to Visualize the Transformations

Graphing is a powerful tool for visualizing transformations. By graphing the parent function and its transformed versions, you can see how the transformations affect the graph.

Here is an example of how graphing can help:

• Graph the parent function f(x) = x^2.
• Graph the function that results from shifting the parent function up 3 units, f(x) = x^2 + 3.
• Compare the two graphs to see how the vertical shift affected the graph.

5. Learn to Identify the Transformation from the Equation

Once you have practiced transforming parent functions, you need to learn how to identify the transformation from the equation. This involves being able to look at an equation and determine what transformation was applied to the parent function.

Here are some tips for identifying transformations from equations:

• Look for the coefficient of the x-term to determine if there is a horizontal shift.
• Look for the constant term to determine if there is a vertical shift.
• Look for a negative sign in front of the function to determine if there is a reflection.

6. Apply Transformations to Real-World Problems

Finally, practice applying transformations to real-world problems. This will help you see the relevance of parent functions and transformations to real-life situations.

Here is an example of a real-world problem that involves transformations:

• A company is producing a new product, and the cost of producing x units is given by the function f(x) = 2x + 5. If the company wants to increase the cost by 10%, what is the new function?

By applying transformations to real-world problems, you can see how parent functions and transformations can be used to model real-world situations.

📝 Note: Mastering parent functions and their transformations takes time and practice. Don't be discouraged if you don't understand it at first. Keep practicing, and you will eventually become proficient.

In conclusion, mastering parent functions and their transformations is essential for any student of mathematics. By identifying the parent function, understanding the transformations, practicing, using graphing to visualize the transformations, learning to identify the transformation from the equation, and applying transformations to real-world problems, you can become proficient in working with parent functions and transformations.

Related Terms:

• Desmos
• Symbolab
• Photomath
• GeoGebra
• Microsoft Math
• Wolfram Alpha