Understanding the Concept of One Solution, No Solution, and Infinite Solutions
When dealing with linear equations, we often come across three types of solutions: one solution, no solution, and infinite solutions. Understanding the difference between these types of solutions is crucial in algebra and other areas of mathematics. In this article, we will explore each type of solution, provide examples, and offer a worksheet to help reinforce your understanding.
One Solution
A linear equation has one solution when it has a unique value that satisfies the equation. In other words, there is only one value of the variable that makes the equation true.
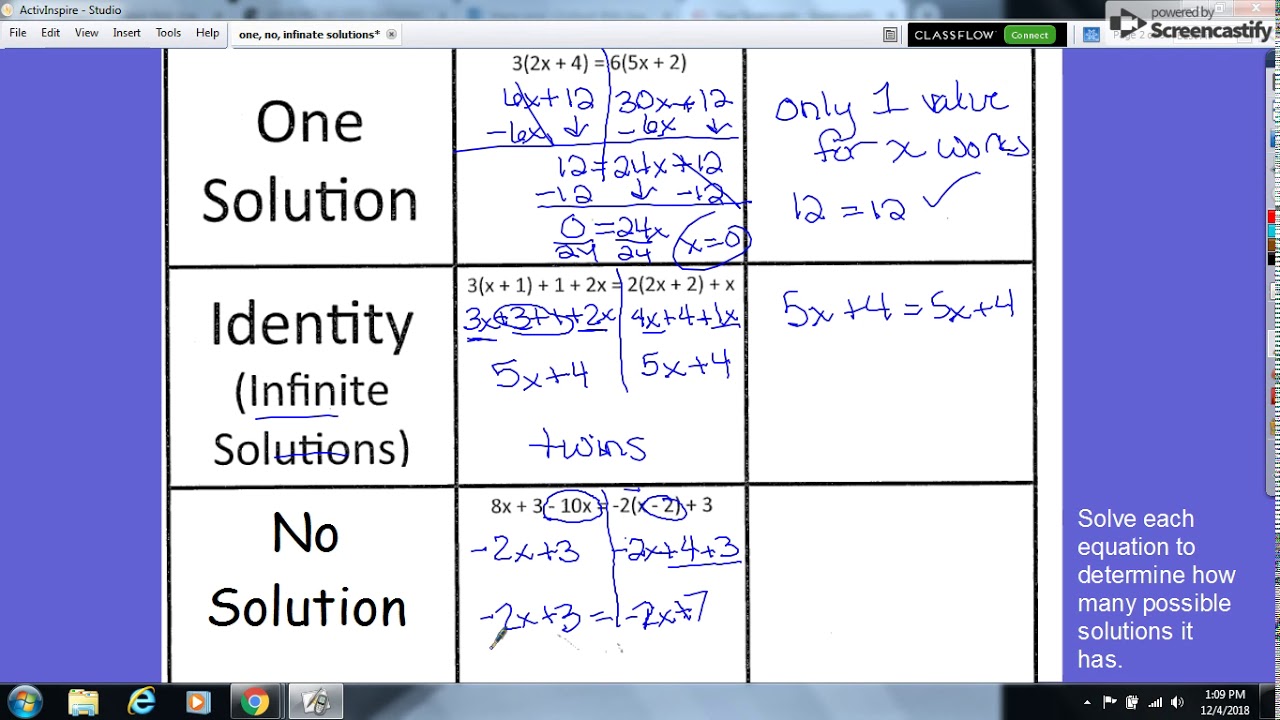
Example: 2x + 3 = 7
To solve for x, we can subtract 3 from both sides of the equation and then divide both sides by 2:
2x = 7 - 3 2x = 4 x = 4⁄2 x = 2
In this example, the equation has one solution, x = 2.
No Solution
A linear equation has no solution when there is no value of the variable that satisfies the equation. This can occur when the equation is a contradiction, such as 0 = 1.
Example: x + 2 = x - 2
Subtracting x from both sides of the equation gives us:
2 = -2
This is a contradiction, and there is no value of x that can make the equation true. Therefore, this equation has no solution.
Infinite Solutions
A linear equation has infinite solutions when it is an identity, meaning that it is true for all values of the variable.
Example: 2x = 2x
This equation is true for all values of x, since the left-hand side and the right-hand side of the equation are the same. Therefore, this equation has infinite solutions.
Worksheet Examples
Here are some worksheet examples to help you practice identifying one solution, no solution, and infinite solutions:
| Equation | Solution |
|---|---|
| x + 4 = 9 | One solution (x = 5) |
| 2x - 2 = 2x + 2 | No solution |
| 3x = 3x | Infinite solutions |
| x/2 + 3 = 7 | One solution (x = 8) |
| x - 2 = x + 2 | No solution |
| 4x = 4x | Infinite solutions |
📝 Note: Remember to check your work and make sure you understand the reasoning behind each solution.
Now that you have a better understanding of one solution, no solution, and infinite solutions, try working through the worksheet examples on your own. Good luck!
What is the difference between one solution and infinite solutions?
+A linear equation has one solution when it has a unique value that satisfies the equation, whereas an equation has infinite solutions when it is an identity, meaning that it is true for all values of the variable.
Can a linear equation have both one solution and infinite solutions?
+No, a linear equation can either have one solution, no solution, or infinite solutions, but not a combination of two or more.
How can I determine if an equation has no solution?
+An equation has no solution when it is a contradiction, such as 0 = 1. You can also check if the equation has no solution by trying to solve it and seeing if you end up with a contradiction.
