Multiplying Rational Expressions Worksheet

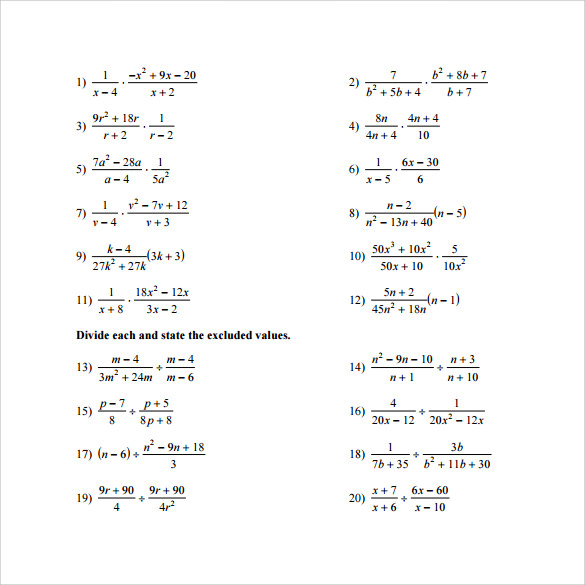
Multiplying Rational Expressions: A Step-by-Step Guide

Multiplying rational expressions is a fundamental concept in algebra, and it’s essential to understand the rules and steps involved in the process. In this worksheet, we’ll walk you through a step-by-step guide on how to multiply rational expressions, along with examples and exercises to help you practice.

What are Rational Expressions?

Rational expressions are fractions that contain polynomials in the numerator and denominator. They are called “rational” because they are the ratio of two polynomials. Rational expressions can be simplified, added, subtracted, multiplied, and divided, just like fractions.

Multiplying Rational Expressions: The Rules

To multiply rational expressions, you need to follow these rules:

• Multiply the numerators (the numbers on top) together.
• Multiply the denominators (the numbers on the bottom) together.
• Simplify the resulting fraction, if possible.

Example 1: Multiplying Rational Expressions

Let’s consider an example:

Multiply the rational expressions:

\[\frac{x+3}{x-2} \cdot \frac{x-1}{x+4}\]

Step 1: Multiply the numerators together:

\[(x+3)(x-1) = x^2 + 3x - x - 3 = x^2 + 2x - 3\]

Step 2: Multiply the denominators together:

\[(x-2)(x+4) = x^2 + 4x - 2x - 8 = x^2 + 2x - 8\]

Step 3: Write the product as a fraction:

\[\frac{x^2 + 2x - 3}{x^2 + 2x - 8}\]

Step 4: Simplify the fraction, if possible. In this case, the fraction cannot be simplified further.

Example 2: Multiplying Rational Expressions with Common Factors

Let’s consider another example:

Multiply the rational expressions:

\[\frac{2x+4}{x+2} \cdot \frac{x+1}{2x-4}\]

Step 1: Factor out any common factors from the numerators and denominators:

\[\frac{2(x+2)}{(x+2)} \cdot \frac{(x+1)}{2(x-2)}\]

Step 2: Cancel out any common factors:

\[\frac{2}{2} \cdot \frac{x+1}{x-2} = \frac{x+1}{x-2}\]

Step 3: Write the product as a fraction:

\[\frac{x+1}{x-2}\]

Step 4: Simplify the fraction, if possible. In this case, the fraction cannot be simplified further.

Exercises

Now it’s your turn to practice! Multiply the following rational expressions:

1. $\frac{x+2}{x-3} \cdot \frac{x-1}{x+1}$
2. $\frac{2x+6}{x+3} \cdot \frac{x-2}{2x-6}$
3. $\frac{x^2 + 4x + 4}{x^2 - 4} \cdot \frac{x+2}{x-2}$
4. $\frac{3x-6}{x-2} \cdot \frac{x+1}{3x-3}$

Notes

📝 Note: When multiplying rational expressions, make sure to factor out any common factors from the numerators and denominators to simplify the process.

📝 Note: Always simplify the resulting fraction, if possible, by canceling out any common factors.

Conclusion

Multiplying rational expressions is a fundamental concept in algebra, and it’s essential to understand the rules and steps involved in the process. By following the rules and practicing with examples, you’ll become more confident and proficient in multiplying rational expressions.