Mastering the Art of Multiplying Multi Digit Numbers
Multiplying multi-digit numbers can be a daunting task for many students, but with practice and the right strategies, it can become a manageable and even enjoyable process. In this article, we will explore five ways to master multiplying multi-digit numbers, from simple to more complex methods.
Method 1: The Standard Algorithm
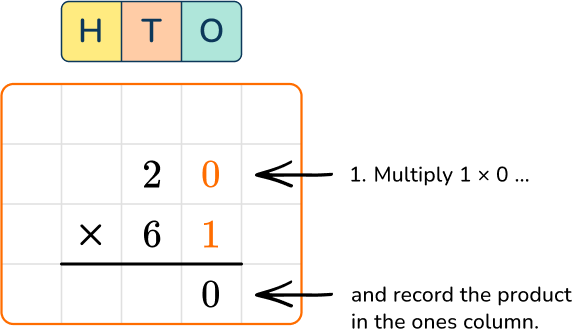
The standard algorithm for multiplying multi-digit numbers involves multiplying each digit of one number by each digit of the other number, and then adding up the products. This method is often taught in schools and is a good starting point for many students.
đź“ť Note: Make sure to line up the digits correctly and use a zero as a placeholder when necessary.
For example, let’s multiply 43 and 27 using the standard algorithm:
43
Ă— 27
------
43 Ă— 20 = 860
43 Ă— 7 = 301
------
1161
Method 2: The Partial Products Method
The partial products method involves breaking down the multiplication problem into smaller parts and calculating each part separately. This method can be helpful for students who struggle with the standard algorithm.
For example, let’s multiply 43 and 27 using the partial products method:
40 Ă— 20 = 800
40 Ă— 7 = 280
3 Ă— 20 = 60
3 Ă— 7 = 21
------
1161
Method 3: The Lattice Method
The lattice method involves creating a grid and calculating the product of each pair of digits. This method can be helpful for students who are visual learners.
| 40 | 3 |
| 20 | 7 |
40 Ă— 20 = 800
40 Ă— 7 = 280
3 Ă— 20 = 60
3 Ă— 7 = 21
------
1161
Method 4: The Box Method
The box method involves creating a series of boxes and calculating the product of each pair of digits. This method can be helpful for students who are struggling to line up digits correctly.
| 40 | 3 |
| 20 | 7 |
40 Ă— 20 = 800
40 Ă— 7 = 280
3 Ă— 20 = 60
3 Ă— 7 = 21
------
1161
Method 5: The Mental Math Method
The mental math method involves using estimation and calculation to multiply multi-digit numbers in your head. This method can be helpful for students who are confident in their math skills and want to improve their mental math abilities.
For example, let’s multiply 43 and 27 using the mental math method:
- Estimate the product: 40 Ă— 20 = 800, 3 Ă— 20 = 60, 3 Ă— 7 = 21
- Calculate the product: 800 + 60 + 21 = 881
- Adjust the estimate: 881 is close to 1161, but not exact. Adjust the estimate by adding 280 (40 Ă— 7) to get 1161.
As you can see, there are many different ways to master multiplying multi-digit numbers. By practicing each method, you can find the one that works best for you and become more confident in your math skills.
Some key points to keep in mind:
- Practice regularly to improve your skills
- Use a variety of methods to find what works best for you
- Don’t be afraid to make mistakes – they are an important part of the learning process
By following these tips and practicing regularly, you can become a master of multiplying multi-digit numbers and improve your math skills overall.
What is the standard algorithm for multiplying multi-digit numbers?
+The standard algorithm involves multiplying each digit of one number by each digit of the other number, and then adding up the products.
What is the partial products method?
+The partial products method involves breaking down the multiplication problem into smaller parts and calculating each part separately.
What is the lattice method?
+The lattice method involves creating a grid and calculating the product of each pair of digits.
