5 Ways to Master Multiplying Mixed Numbers

Mastering the Art of Multiplying Mixed Numbers
Multiplying mixed numbers can be a daunting task for many students, but with the right approach, it can become a breeze. Mixed numbers are a combination of a whole number and a fraction, and multiplying them requires a step-by-step process. In this article, we will explore five ways to master multiplying mixed numbers, making you a pro in no time.
Method 1: Converting to Improper Fractions
The first method is to convert the mixed numbers to improper fractions. This involves multiplying the whole number by the denominator and adding the numerator to get the new numerator.
For example, let’s say we want to multiply 2 1⁄3 and 3 3⁄4. We can convert these mixed numbers to improper fractions:
2 1⁄3 = (2 x 3) + 1 = 7⁄3 3 3⁄4 = (3 x 4) + 3 = 15⁄4
Now, we can multiply the numerators and denominators:
(7⁄3) x (15⁄4) = 105⁄12
To simplify, we can convert the improper fraction back to a mixed number:
105⁄12 = 8 9⁄12
📝 Note: When converting mixed numbers to improper fractions, make sure to multiply the whole number by the denominator and add the numerator to get the new numerator.
Method 2: Using a Grid or Area Model
Another way to multiply mixed numbers is by using a grid or area model. This method involves creating a grid with the whole numbers and fractions, and then multiplying the corresponding parts.
For example, let’s say we want to multiply 2 1⁄3 and 3 3⁄4. We can create a grid:
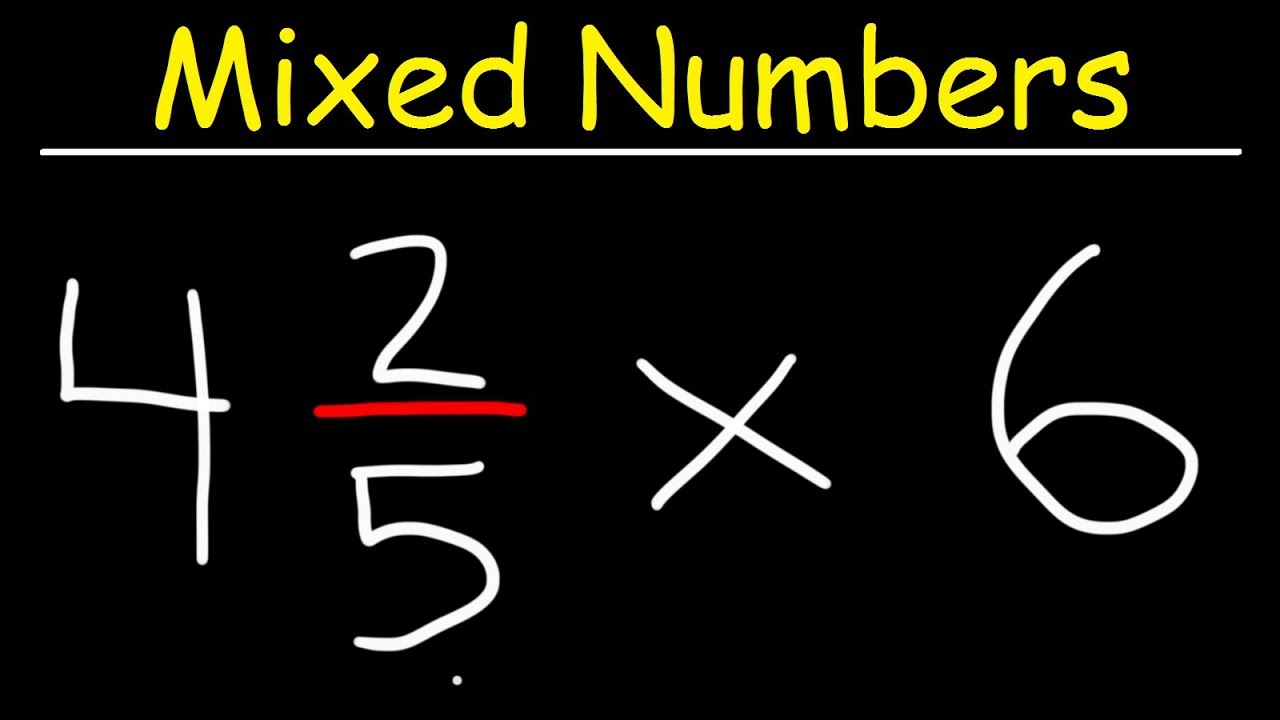
| 2 | 1⁄3 | |
|---|---|---|
| 3 | 6 | 3⁄4 |
| 3⁄4 | 9⁄4 | 1⁄12 |
Now, we can multiply the corresponding parts:
6 x 3 = 18 6 x 3⁄4 = 9⁄2 3⁄4 x 1⁄3 = 1⁄12
Adding up the products, we get:
18 + 9⁄2 + 1⁄12 = 105⁄12
📝 Note: When using the grid or area model, make sure to multiply the corresponding parts and add up the products.
Method 3: Using the Standard Algorithm
The standard algorithm for multiplying mixed numbers involves multiplying the whole numbers and fractions separately, and then adding the products.
For example, let’s say we want to multiply 2 1⁄3 and 3 3⁄4. We can multiply the whole numbers and fractions separately:
2 x 3 = 6 1⁄3 x 3⁄4 = 1⁄12
Now, we can add the products:
6 + 1⁄12 = 105⁄12
📝 Note: When using the standard algorithm, make sure to multiply the whole numbers and fractions separately, and then add the products.
Method 4: Using Real-World Applications
Multiplying mixed numbers can be applied to real-world situations, such as cooking or measuring ingredients. By using real-world applications, students can visualize the concept of multiplying mixed numbers.
For example, let’s say we want to multiply 2 1⁄3 cups of flour and 3 3⁄4 cups of sugar. We can create a real-world scenario:
Imagine we are baking a cake that requires 2 1⁄3 cups of flour and 3 3⁄4 cups of sugar. If we want to make 3 batches of the cake, how much flour and sugar do we need?
By multiplying the mixed numbers, we can get the total amount of flour and sugar needed:
(2 1⁄3) x 3 = 7 1⁄3 cups of flour (3 3⁄4) x 3 = 11 1⁄4 cups of sugar
📝 Note: When using real-world applications, make sure to create a scenario that visualizes the concept of multiplying mixed numbers.
Method 5: Practicing with Online Resources
Finally, practicing with online resources can help students master multiplying mixed numbers. There are many online resources available, such as math games, worksheets, and video tutorials.
For example, students can practice multiplying mixed numbers using online worksheets or math games. These resources can provide a fun and interactive way to learn the concept of multiplying mixed numbers.
📝 Note: When practicing with online resources, make sure to find resources that are engaging and interactive.
Multiplying mixed numbers can be a challenging concept for many students, but by using these five methods, students can master the concept in no time. Whether it’s converting to improper fractions, using a grid or area model, using the standard algorithm, using real-world applications, or practicing with online resources, students can become proficient in multiplying mixed numbers.
Now, let’s summarize the key points:
- Converting mixed numbers to improper fractions can help simplify the multiplication process.
- Using a grid or area model can help visualize the concept of multiplying mixed numbers.
- The standard algorithm involves multiplying the whole numbers and fractions separately, and then adding the products.
- Real-world applications can help students visualize the concept of multiplying mixed numbers.
- Practicing with online resources can provide a fun and interactive way to learn the concept of multiplying mixed numbers.
What is the best way to multiply mixed numbers?
+The best way to multiply mixed numbers is to use a combination of methods, such as converting to improper fractions, using a grid or area model, and practicing with online resources.
Why is multiplying mixed numbers important?
+Multiplying mixed numbers is important because it is used in real-world applications, such as cooking, measuring ingredients, and calculating quantities.
Can I use online resources to practice multiplying mixed numbers?
+Yes, there are many online resources available that can help you practice multiplying mixed numbers, such as math games, worksheets, and video tutorials.