5 Ways to Solve Multi Step Inequalities
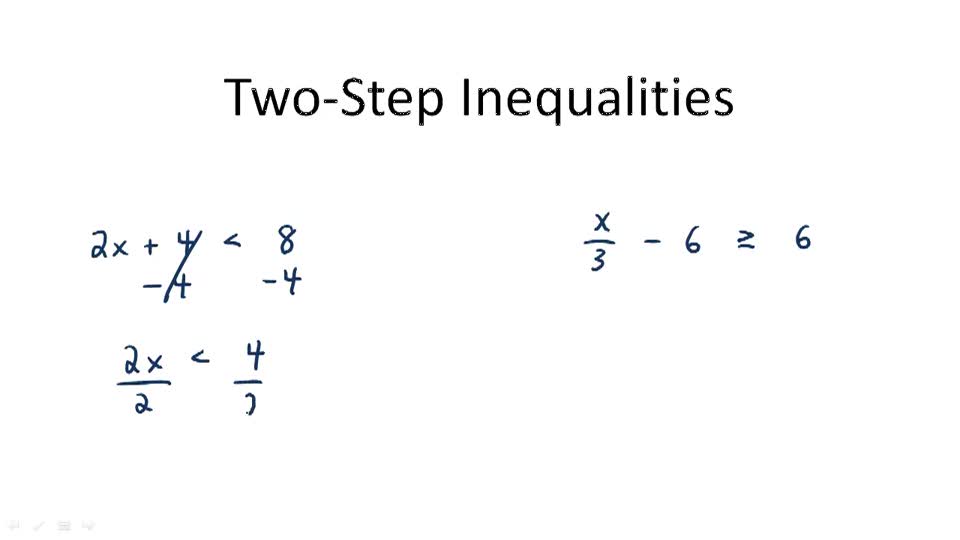
Introduction to Multi-Step Inequalities
Inequalities are a crucial part of algebra, and solving them is an essential skill for any math student. While simple inequalities can be solved in a single step, multi-step inequalities require more effort and strategy. In this post, we’ll explore five ways to solve multi-step inequalities, along with examples and explanations to help you master this skill.
Understanding Multi-Step Inequalities
Before we dive into the solutions, let’s understand what multi-step inequalities are. These are inequalities that require more than one operation to solve, such as addition, subtraction, multiplication, or division. They often involve variables on both sides of the inequality, making them more challenging to solve.
Method 1: Isolate the Variable
The first method to solve multi-step inequalities is to isolate the variable on one side of the inequality. This involves performing inverse operations to get the variable alone.
📝 Note: Inverse operations are opposite operations, such as addition and subtraction, or multiplication and division.
Example: Solve for x in the inequality 2x + 5 > 11
To isolate x, we’ll subtract 5 from both sides, then divide both sides by 2:
2x + 5 > 11 2x > 11 - 5 2x > 6 x > 6⁄2 x > 3
Method 2: Use the Distributive Property
The distributive property is a powerful tool for solving multi-step inequalities. It allows us to expand expressions and simplify the inequality.
Example: Solve for x in the inequality 3(x - 2) < 12
Using the distributive property, we’ll expand the left side of the inequality:
3(x - 2) < 12 3x - 6 < 12 3x < 12 + 6 3x < 18 x < 18⁄3 x < 6
Method 3: Combine Like Terms
When solving multi-step inequalities, it’s essential to combine like terms to simplify the inequality.
Example: Solve for x in the inequality 2x + 3x - 2 > 5
Combining like terms on the left side of the inequality:
2x + 3x - 2 > 5 5x - 2 > 5 5x > 5 + 2 5x > 7 x > 7⁄5
Method 4: Use the Properties of Inequalities
Inequalities have properties that can be used to solve them. One of these properties is the multiplication property, which states that if we multiply or divide both sides of an inequality by the same value, the inequality remains true.
Example: Solve for x in the inequality -4x > 12
Using the multiplication property, we’ll divide both sides of the inequality by -4:
-4x > 12 x < -12⁄4 x < -3
Method 5: Use a Table or Graph
For more complex multi-step inequalities, it can be helpful to use a table or graph to visualize the solution.
Example: Solve for x in the inequality |x - 2| > 3
Using a table to find the values of x that satisfy the inequality:
| x | |x - 2| |
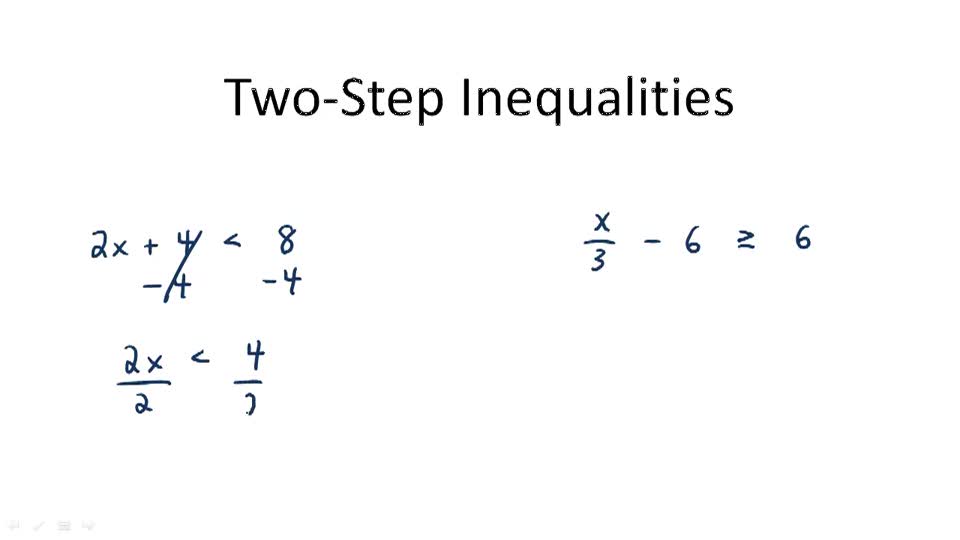
| 0 | 2 | No |
| 1 | 1 | No |
| 2 | 0 | No |
| 3 | 1 | No |
| 4 | 2 | No |
| 5 | 3 | Yes |
From the table, we can see that x > 5 or x < -1.
In conclusion, solving multi-step inequalities requires a combination of algebraic skills and strategic thinking. By using these five methods, you’ll be able to tackle even the most challenging inequalities with confidence. Remember to always check your solutions and consider multiple methods to ensure you’ve found the correct answer.
What is the difference between a simple inequality and a multi-step inequality?
+A simple inequality requires only one operation to solve, while a multi-step inequality requires more than one operation.
What is the distributive property, and how is it used in solving inequalities?
+The distributive property allows us to expand expressions by multiplying each term inside the parentheses by the term outside the parentheses. This property is useful in solving inequalities by simplifying the left side of the inequality.
How do I know which method to use when solving a multi-step inequality?
+The method you choose will depend on the specific inequality you’re trying to solve. Look for clues such as like terms, distributive property, or properties of inequalities to determine the best approach.