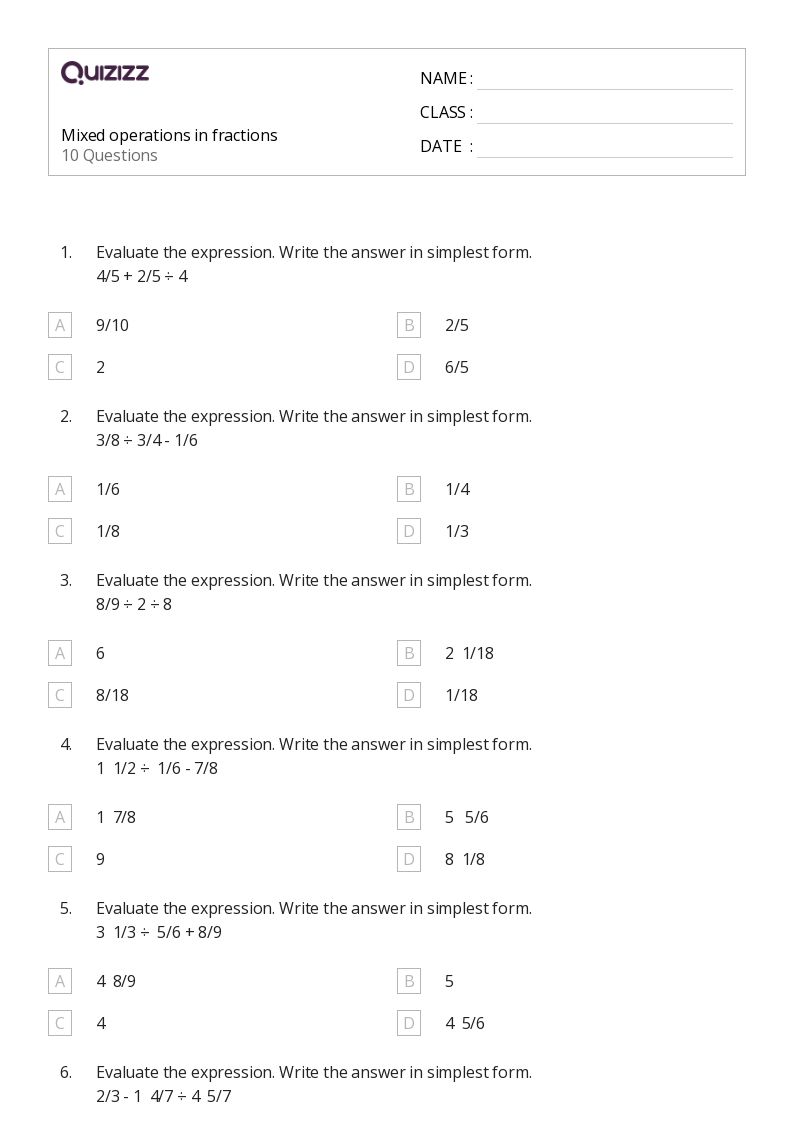
5 Mixed Operations on Fractions You Need to Master
Understanding Fractions and Mixed Operations
Fractions are a fundamental concept in mathematics, representing a part of a whole. Mixed operations on fractions involve combining different arithmetic operations, such as addition, subtraction, multiplication, and division, to solve problems. Mastering these mixed operations is crucial for students to excel in mathematics and real-world applications. In this article, we will explore five mixed operations on fractions that you need to master.
1. Adding and Subtracting Fractions with Unlike Denominators
When adding or subtracting fractions with unlike denominators, we need to find the least common multiple (LCM) of the denominators. The LCM is the smallest number that both denominators can divide into evenly.
📝 Note: To find the LCM, list the multiples of each denominator and identify the smallest number that appears in both lists.
For example, let’s add 1⁄4 and 1⁄6:

| Fraction | Denominator |
|---|---|
| 1/4 | 4 |
| 1/6 | 6 |
The LCM of 4 and 6 is 12. Now, convert each fraction to have a denominator of 12:
1⁄4 = 3⁄12 1⁄6 = 2⁄12
Add the fractions:
3⁄12 + 2⁄12 = 5⁄12
2. Multiplying and Dividing Fractions
To multiply fractions, multiply the numerators and multiply the denominators. To divide fractions, invert the second fraction (i.e., flip the numerator and denominator) and multiply.
For example, let’s multiply 1⁄2 and 3⁄4:
1⁄2 × 3⁄4 = (1 × 3) / (2 × 4) = 3⁄8
Now, let’s divide 1⁄2 by 3⁄4:
1⁄2 ÷ 3⁄4 = 1⁄2 × 4⁄3 = (1 × 4) / (2 × 3) = 4⁄6
3. Adding, Subtracting, Multiplying, and Dividing Mixed Numbers
Mixed numbers consist of a whole number and a fraction. To add, subtract, multiply, or divide mixed numbers, convert them to improper fractions and perform the operation.
For example, let’s add 2 1⁄2 and 1 3⁄4:
Convert to improper fractions:
2 1⁄2 = 5⁄2 1 3⁄4 = 7⁄4
Add the fractions:
5⁄2 + 7⁄4 = (5 × 2) / (2 × 2) + (7 × 1) / (4 × 1) = 10⁄4 + 7⁄4 = 17⁄4
4. Simplifying Complex Fractions
Complex fractions involve fractions within fractions. To simplify complex fractions, convert them to division problems and perform the operation.
For example, let’s simplify:
(1⁄2) / (3⁄4)
Invert the second fraction and multiply:
(1⁄2) × (4⁄3) = (1 × 4) / (2 × 3) = 4⁄6
5. Solving Word Problems Involving Mixed Operations on Fractions
Word problems involving mixed operations on fractions require you to read the problem carefully and apply the correct operations.
For example, let’s solve:
Tom has 1⁄2 cup of sugar. He adds 1⁄4 cup of sugar to the mixture. Later, he needs to divide the mixture into 3 equal parts. How much sugar will each part contain?
Add the fractions:
1⁄2 + 1⁄4 = 3⁄4
Divide the mixture into 3 equal parts:
3⁄4 ÷ 3 = 1⁄4
Each part will contain 1⁄4 cup of sugar.
In conclusion, mastering mixed operations on fractions is essential for mathematical problem-solving. By understanding how to add, subtract, multiply, and divide fractions, as well as simplifying complex fractions and solving word problems, you’ll become proficient in working with fractions and mixed numbers.
What is the least common multiple (LCM)?
+The LCM is the smallest number that both denominators can divide into evenly.
How do I add fractions with unlike denominators?
+Find the LCM of the denominators, convert each fraction to have the LCM as the denominator, and add the fractions.
What is the difference between multiplying and dividing fractions?
+Multiplying fractions involves multiplying the numerators and denominators, while dividing fractions involves inverting the second fraction and multiplying.



