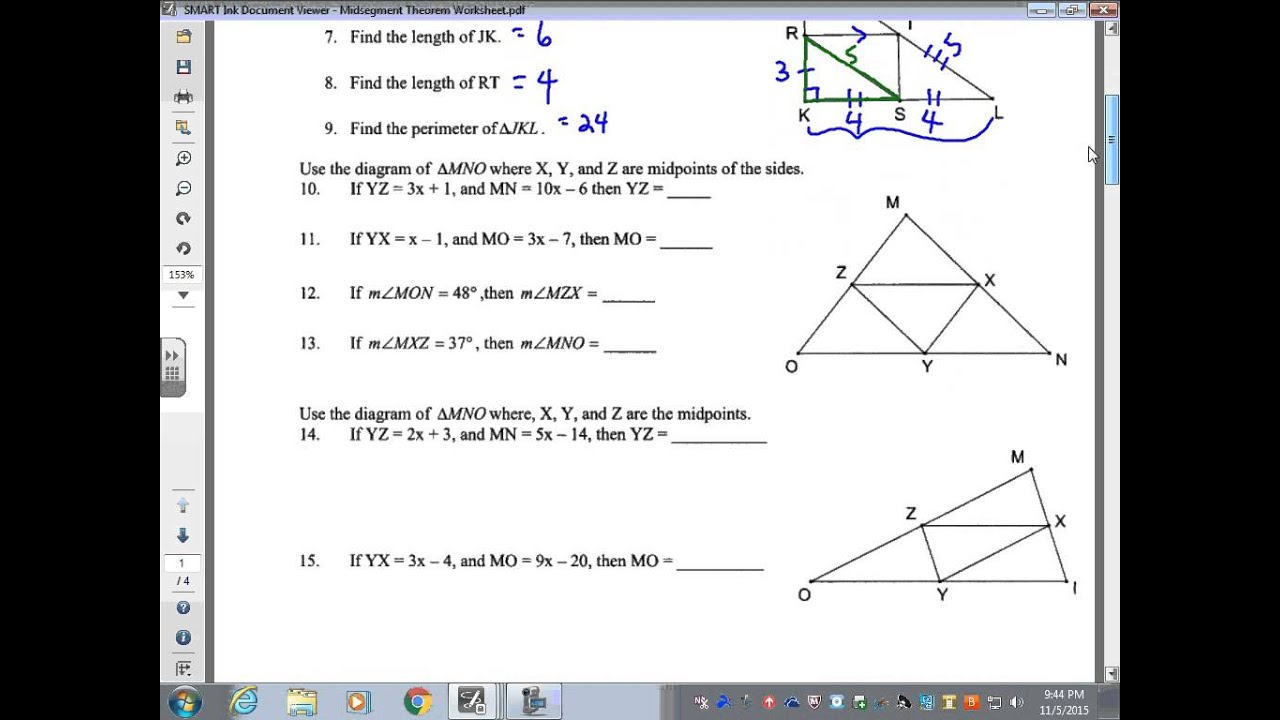
Midsegment Triangle Worksheet

Understanding the Midsegment of a Triangle
The midsegment of a triangle is a line segment that joins the midpoints of two sides of a triangle. It is a fundamental concept in geometry, and it has several important properties that make it useful in various mathematical and real-world applications.
What is a Midsegment?
A midsegment is a line segment that connects the midpoints of two sides of a triangle. For example, in triangle ABC, the midsegment can be the line segment that joins the midpoints of sides AB and AC.
Properties of a Midsegment
The midsegment of a triangle has several important properties:
- Parallel to the Third Side: The midsegment is always parallel to the third side of the triangle.
- Half the Length of the Third Side: The midsegment is always half the length of the third side of the triangle.
- Bisects the Area of the Triangle: The midsegment divides the triangle into two smaller triangles of equal area.
How to Find the Midsegment of a Triangle
To find the midsegment of a triangle, follow these steps:
- Identify the midpoints of two sides of the triangle.
- Draw a line segment that connects the midpoints.
- Verify that the line segment is parallel to the third side of the triangle.
Midsegment Theorem
The midsegment theorem states that the midsegment of a triangle is parallel to the third side of the triangle and is half the length of the third side. This theorem can be used to find the length of the midsegment if the length of the third side is known.
Examples of Midsegment in Real-World Applications
The midsegment of a triangle has several real-world applications, including:
- Architecture: The midsegment can be used to design buildings and bridges with symmetrical features.
- Engineering: The midsegment can be used to calculate the stress and strain on beams and girders.
- Computer Graphics: The midsegment can be used to create 3D models with symmetrical features.
Worksheets and Exercises
Here are some worksheets and exercises to help you practice finding the midsegment of a triangle:
| Triangle | Midsegment | Length of Midsegment |
|---|---|---|
| ABC | DE | Half the length of BC |
| DEF | GH | Half the length of EF |
| JKL | MN | Half the length of KL |
📝 Note: The length of the midsegment is always half the length of the third side of the triangle.
Conclusion
In conclusion, the midsegment of a triangle is a fundamental concept in geometry with several important properties and real-world applications. By understanding the properties of the midsegment and how to find it, you can apply it to various mathematical and real-world problems.
What is the midsegment of a triangle?
+The midsegment of a triangle is a line segment that joins the midpoints of two sides of a triangle.
What are the properties of a midsegment?
+The midsegment is always parallel to the third side of the triangle, half the length of the third side, and bisects the area of the triangle.
How do I find the midsegment of a triangle?
+To find the midsegment of a triangle, identify the midpoints of two sides, draw a line segment that connects the midpoints, and verify that the line segment is parallel to the third side of the triangle.