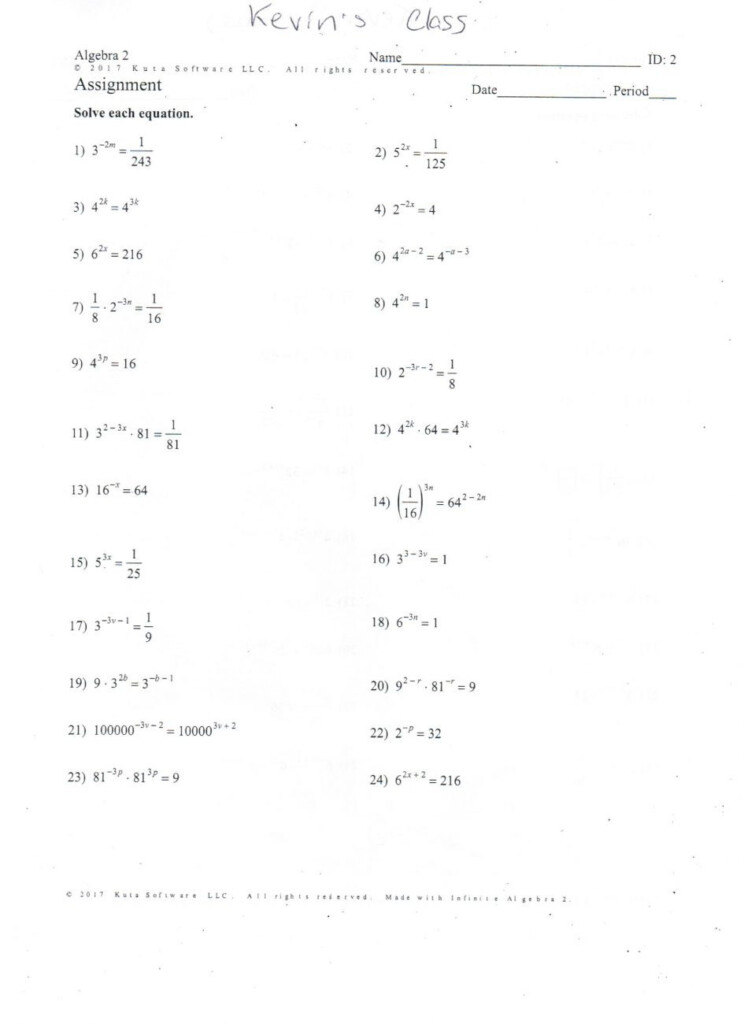Linear Equations Standard Form Worksheet Solutions

Understanding Linear Equations in Standard Form
Linear equations are a fundamental concept in mathematics, and understanding how to work with them is crucial for problem-solving in various fields. One of the most common forms of linear equations is the standard form, which is represented as Ax + By = C, where A, B, and C are constants. In this article, we will delve into the world of linear equations in standard form, exploring the concept, benefits, and how to work with them.
What are Linear Equations in Standard Form?
Linear equations in standard form are equations that can be written in the form Ax + By = C, where:
- A and B are coefficients of the variables x and y, respectively
- C is a constant term
- x and y are the variables
For example, 2x + 3y = 5 is a linear equation in standard form.
Benefits of Standard Form
Linear equations in standard form have several benefits, including:
- Easy to compare: Standard form makes it easy to compare two or more linear equations.
- Simple to add or subtract: Adding or subtracting linear equations in standard form is straightforward.
- Easy to solve: Standard form makes it easy to solve linear equations using various methods, such as graphing or substitution.
How to Convert Linear Equations to Standard Form
Converting linear equations to standard form is a simple process. Here are the steps:
- Write the equation in the form Ax + By = C.
- Ensure that the coefficients of the variables (A and B) are integers.
- If the coefficients are not integers, multiply the entire equation by the least common multiple (LCM) of the denominators.
For example, convert the equation 1/2x + 3/4y = 2 to standard form:
- Multiply the entire equation by the LCM of the denominators, which is 4: 2x + 3y = 8
- The equation is now in standard form.
Solving Linear Equations in Standard Form
Solving linear equations in standard form is a straightforward process. Here are the steps:
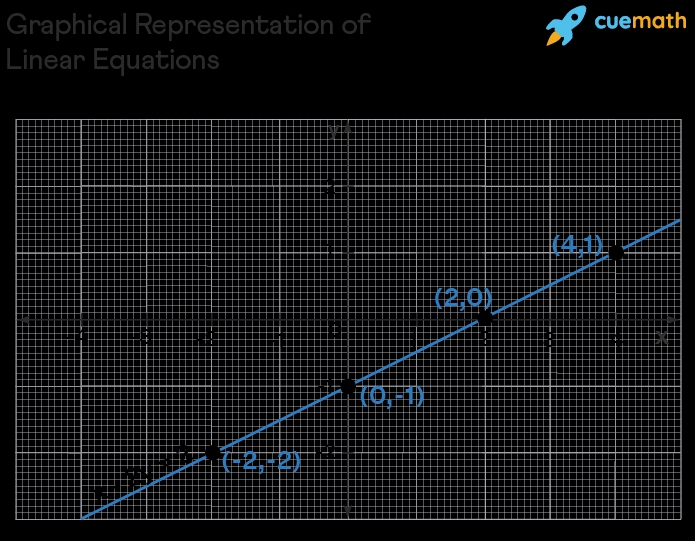
- Graphing method: Plot the equation on a graph and find the point of intersection with the x-axis or y-axis.
- Substitution method: Substitute one variable in terms of the other and solve for the remaining variable.
- Elimination method: Add or subtract the equations to eliminate one variable and solve for the remaining variable.
For example, solve the equation 2x + 3y = 5 using the substitution method:
- Solve for y in terms of x: y = (5 - 2x) / 3
- Substitute y into another equation or use the equation to find the value of x.
Worksheet Solutions
Here are the solutions to some linear equations in standard form:
| Equation | Solution |
|---|---|
| 2x + 3y = 5 | y = (5 - 2x) / 3 |
| x - 2y = -3 | x = -3 + 2y |
| 4x + 2y = 8 | y = (8 - 4x) / 2 |
📝 Note: These solutions can be obtained using various methods, including graphing, substitution, or elimination.
In conclusion, linear equations in standard form are a fundamental concept in mathematics, and understanding how to work with them is crucial for problem-solving in various fields. By following the steps outlined in this article, you can convert linear equations to standard form, solve them using various methods, and apply them to real-world problems.
What is the standard form of a linear equation?
+The standard form of a linear equation is Ax + By = C, where A, B, and C are constants.
How do I convert a linear equation to standard form?
+To convert a linear equation to standard form, write the equation in the form Ax + By = C, ensure that the coefficients of the variables (A and B) are integers, and multiply the entire equation by the least common multiple (LCM) of the denominators if necessary.
What are some methods for solving linear equations in standard form?
+Some methods for solving linear equations in standard form include graphing, substitution, and elimination.
Related Terms:
- Graphing Linear Equations Worksheet