Mastering Triangles: Law of Sines and Cosines Worksheet
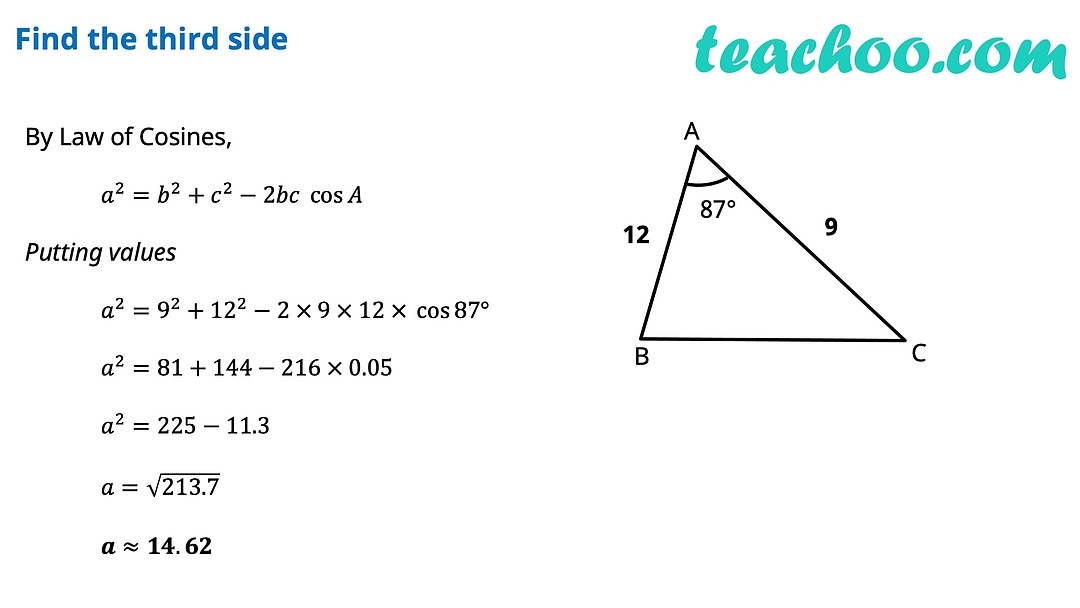
Unlocking the Secrets of Triangles: A Comprehensive Guide to the Law of Sines and Cosines
Triangles are the building blocks of geometry, and understanding their properties is crucial for solving various mathematical problems. Two essential tools for navigating the world of triangles are the Law of Sines and the Law of Cosines. In this article, we will delve into the world of triangles, exploring the Law of Sines and Cosines, and provide a worksheet to help you master these concepts.
What is the Law of Sines?
The Law of Sines is a fundamental concept in trigonometry that relates the lengths of the sides of a triangle to the sines of its angles. The law states that for any triangle with angles A, B, and C, and opposite sides a, b, and c, respectively:
a / sin(A) = b / sin(B) = c / sin©
This equation allows you to find the length of a side of a triangle if you know the measure of one of its angles and the length of the other two sides.
What is the Law of Cosines?
The Law of Cosines is another essential concept in trigonometry that relates the lengths of the sides of a triangle to the cosine of one of its angles. The law states that for any triangle with sides a, b, and c, and angle C opposite side c:
c² = a² + b² - 2ab * cos©
This equation allows you to find the length of the third side of a triangle if you know the lengths of the other two sides and the measure of the angle between them.
Using the Law of Sines and Cosines: Examples and Applications
Let’s consider a few examples to illustrate the use of the Law of Sines and Cosines:
- Example 1: In a triangle, the measure of angle A is 60°, and the length of side a is 10 units. If the length of side b is 15 units, find the measure of angle B.
Using the Law of Sines:
10 / sin(60°) = 15 / sin(B)
Solving for sin(B), we get:
sin(B) = 15 * sin(60°) / 10
B ≈ 77.32°
- Example 2: In a triangle, the lengths of sides a and b are 7 units and 9 units, respectively, and the measure of angle C is 120°. Find the length of side c.
Using the Law of Cosines:
c² = 7² + 9² - 2 * 7 * 9 * cos(120°)
Solving for c, we get:
c ≈ 11.37 units
Mastering Triangles: Law of Sines and Cosines Worksheet
Now it’s your turn to practice! Complete the following worksheet to test your understanding of the Law of Sines and Cosines.
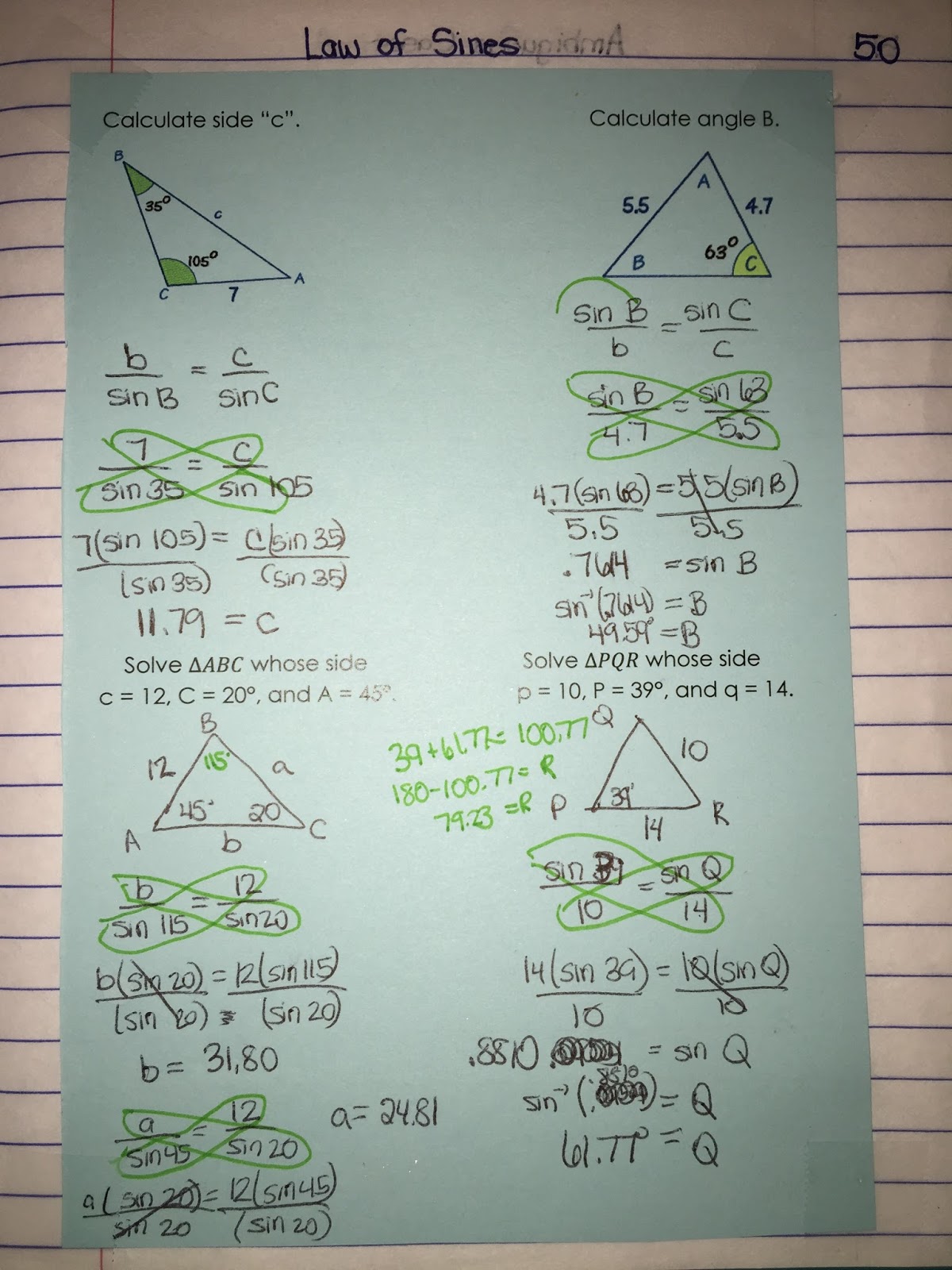
| Problem | Given Information | Find |
|---|---|---|
| 1 | Angle A = 45°, side a = 8 units | Measure of angle B |
| 2 | Sides a = 5 units, b = 12 units, angle C = 90° | Length of side c |
| 3 | Angle B = 30°, side b = 10 units | Measure of angle A |
| 4 | Sides a = 9 units, b = 7 units, angle C = 60° | Length of side c |
| 5 | Angle A = 75°, side a = 11 units | Measure of angle B |
Answer Key
- Measure of angle B ≈ 65.51°
- Length of side c ≈ 13 units
- Measure of angle A ≈ 60°
- Length of side c ≈ 10.25 units
- Measure of angle B ≈ 42.35°
Final Thoughts
Mastering the Law of Sines and Cosines is essential for solving various mathematical problems involving triangles. With practice and patience, you can become proficient in using these concepts to find unknown sides and angles of triangles. Remember to use the given information and the formulas to solve problems, and don’t hesitate to ask for help if you’re stuck.
What is the difference between the Law of Sines and the Law of Cosines?
+The Law of Sines relates the lengths of the sides of a triangle to the sines of its angles, while the Law of Cosines relates the lengths of the sides of a triangle to the cosine of one of its angles.
How do I know which law to use in a given problem?
+If you know the measure of one angle and the length of the other two sides, use the Law of Sines. If you know the lengths of two sides and the measure of the angle between them, use the Law of Cosines.
Can I use the Law of Sines and Cosines to find the area of a triangle?
+Yes, you can use the Law of Sines to find the area of a triangle if you know the lengths of two sides and the measure of the included angle. However, the Law of Cosines is not typically used to find the area of a triangle.