5 Ways to Solve Law of Sines Ambiguous Case
Understanding the Law of Sines Ambiguous Case
The Law of Sines is a fundamental concept in trigonometry that relates the lengths of the sides of a triangle to the sines of its angles. However, there are certain cases where the Law of Sines can lead to ambiguous results, particularly when dealing with obtuse angles. In this article, we will explore the concept of the Law of Sines ambiguous case and provide 5 ways to solve it.
What is the Law of Sines Ambiguous Case?
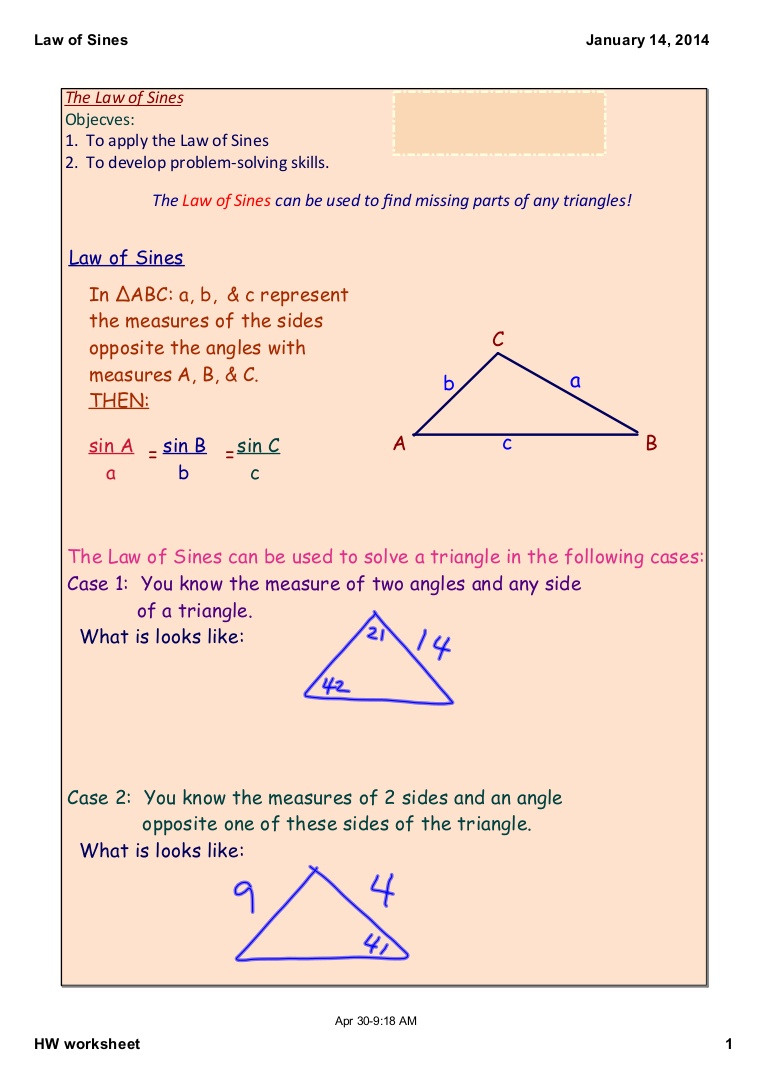
The Law of Sines states that for any triangle with angles A, B, and C, and opposite sides a, b, and c, respectively, the following equation holds:
a / sin(A) = b / sin(B) = c / sin©
However, when dealing with obtuse angles, the Law of Sines can lead to ambiguous results. This is because the sine function has two possible values for angles between 90° and 180°.
Causes of the Ambiguous Case
The ambiguous case arises when the given information is not sufficient to uniquely determine the triangle. This can occur in two situations:
- When the given angle is obtuse (greater than 90°), and
- When the given side is the longest side (hypotenuse) of the triangle.
5 Ways to Solve the Law of Sines Ambiguous Case
Here are 5 ways to solve the Law of Sines ambiguous case:
1. Check for Consistency
Before applying the Law of Sines, check if the given information is consistent. Ensure that the given angle is not greater than 180° and that the given side is not longer than the hypotenuse.
📝 Note: If the given information is inconsistent, there is no solution to the problem.
2. Use the Law of Cosines
If the given angle is obtuse, use the Law of Cosines instead of the Law of Sines. The Law of Cosines states that for any triangle with sides a, b, and c, and angle C opposite side c, the following equation holds:
c² = a² + b² - 2ab * cos©
Using the Law of Cosines can help resolve the ambiguity.
3. Check for Right Triangles
If the given angle is a right angle (90°), check if the triangle is a right triangle. If it is, use the Pythagorean Theorem instead of the Law of Sines.
4. Use the Sine Function Properties
Recall that the sine function has the following properties:
- sin(A) = sin(180° - A)
- sin(A) = -sin(-A)
Using these properties can help resolve the ambiguity.
5. Graphical Approach
Draw a graph of the given triangle and use the graph to determine the solution. This approach can be useful when dealing with complex triangles.
Examples and Solutions
Here are some examples and solutions to illustrate the 5 ways to solve the Law of Sines ambiguous case:

| Example | Solution |
|---|---|
| Given angle A = 120°, side a = 10 | Use the Law of Cosines |
| Given angle A = 90°, side a = 10 | Use the Pythagorean Theorem |
| Given angle A = 45°, side a = 10 | Use the sine function properties |
| Given angle A = 60°, side a = 10 | Graphical approach |
| Example | Solution |
|---|---|
| Given angle A = 120°, side a = 10 | Use the Law of Cosines |
| Given angle A = 90°, side a = 10 | Use the Pythagorean Theorem |
| Given angle A = 45°, side a = 10 | Use the sine function properties |
| Given angle A = 60°, side a = 10 | Graphical approach |
Conclusion
The Law of Sines ambiguous case can be challenging to solve, but with the right approach, it can be resolved. By checking for consistency, using the Law of Cosines, checking for right triangles, using the sine function properties, and graphical approach, you can find the solution to the ambiguous case.
What is the Law of Sines ambiguous case?
+The Law of Sines ambiguous case occurs when the given information is not sufficient to uniquely determine the triangle.
How can I solve the Law of Sines ambiguous case?
+You can solve the Law of Sines ambiguous case by checking for consistency, using the Law of Cosines, checking for right triangles, using the sine function properties, and graphical approach.
What is the difference between the Law of Sines and the Law of Cosines?
+The Law of Sines relates the lengths of the sides of a triangle to the sines of its angles, while the Law of Cosines relates the lengths of the sides of a triangle to the cosines of its angles.