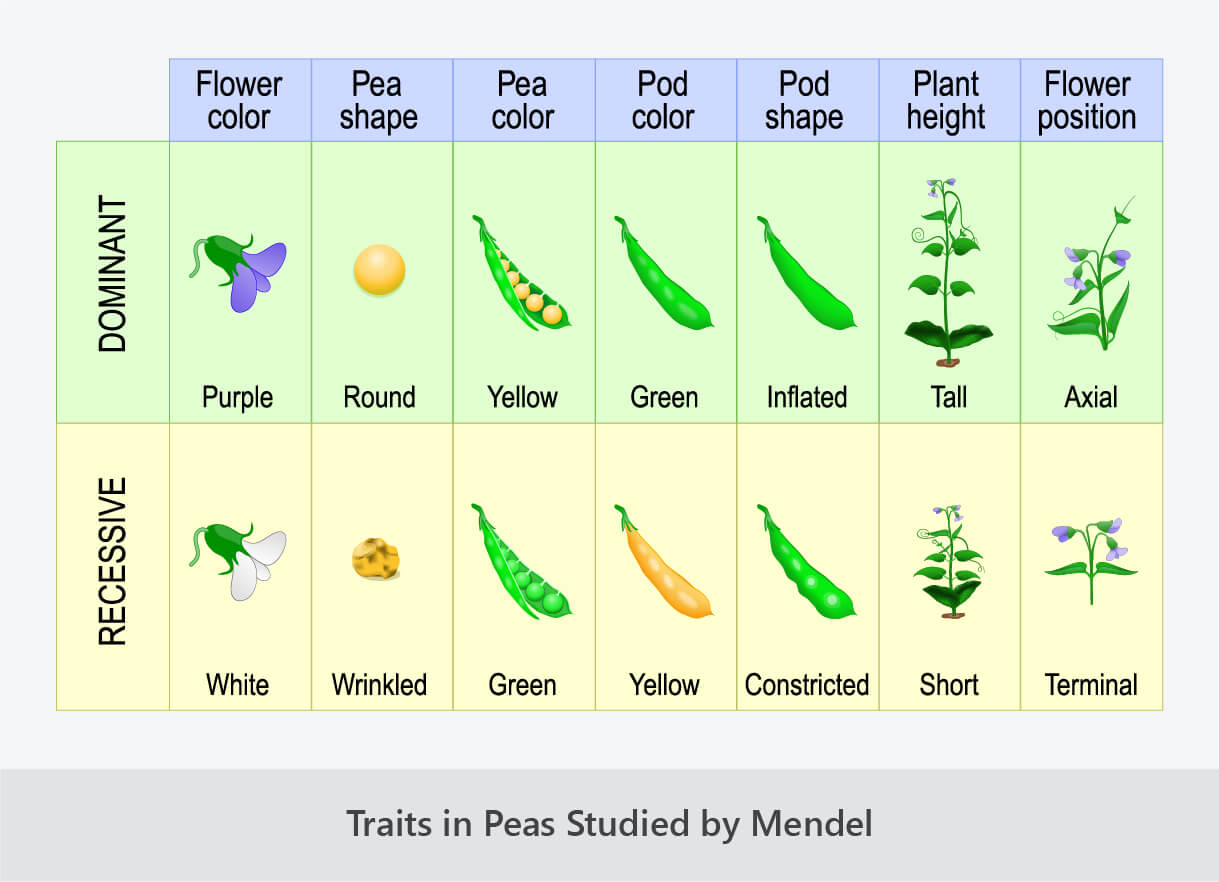
Law of Cosine Worksheet Problems and Solutions
Understanding the Law of Cosines
The Law of Cosines is a fundamental concept in trigonometry that helps you find the length of the third side of a triangle when you know the lengths of the other two sides and the angle between them. This law is useful in various fields, including physics, engineering, and architecture. In this worksheet, we will explore some problems and solutions related to the Law of Cosines.
What is the Law of Cosines?
The Law of Cosines states that for any triangle with sides of length a, b, and c, and an angle C opposite side c, the following equation holds:
c² = a² + b² - 2ab * cos©
This equation allows you to calculate the length of side c when you know the lengths of sides a and b, and the angle C between them.
Problem 1: Finding the Length of the Third Side
In a triangle, the length of side a is 5 cm, the length of side b is 7 cm, and the angle between them is 60°. Find the length of the third side c.
🤔 Note: Use the Law of Cosines to solve this problem.
Solution:
Using the Law of Cosines equation, we can plug in the values:
c² = 5² + 7² - 2(5)(7) * cos(60°) c² = 25 + 49 - 70 * 0.5 c² = 74 - 35 c² = 39 c = √39 ≈ 6.24 cm
Therefore, the length of the third side c is approximately 6.24 cm.
Problem 2: Finding the Angle Between Two Sides
In a triangle, the length of side a is 8 cm, the length of side b is 10 cm, and the length of side c is 12 cm. Find the angle between sides a and b.
🤔 Note: Use the Law of Cosines to solve this problem.
Solution:
Using the Law of Cosines equation, we can rearrange it to solve for the angle:
cos© = (a² + b² - c²) / 2ab cos© = (8² + 10² - 12²) / 2(8)(10) cos© = (64 + 100 - 144) / 160 cos© = 20 / 160 cos© = 1⁄8 C ≈ 82.8°
Therefore, the angle between sides a and b is approximately 82.8°.
Problem 3: Finding the Length of the Third Side (Ambiguous Case)
In a triangle, the length of side a is 3 cm, the length of side b is 4 cm, and the angle between them is 120°. Find the length of the third side c.
🤔 Note: This is an ambiguous case, as there may be two possible solutions.
Solution:
Using the Law of Cosines equation, we can plug in the values:
c² = 3² + 4² - 2(3)(4) * cos(120°) c² = 9 + 16 - 24 * (-0.5) c² = 25 + 12 c² = 37 c = √37 ≈ 6.08 cm or c = -√37 ≈ -6.08 cm ( rejected as length cannot be negative)
However, there is another possible solution:
c² = 3² + 4² - 2(3)(4) * cos(120°) c² = 9 + 16 - 24 * (-0.5) c² = 25 + 12 c² = 37 c = √37 ≈ 6.08 cm or c = -√37 ≈ -6.08 cm ( rejected as length cannot be negative) c = √(37 + 24) ≈ 8.06 cm (another possible solution)
Therefore, there are two possible lengths for the third side c: approximately 6.08 cm and 8.06 cm.
| Problem | Given Values | Solution |
|---|---|---|
| 1 | a = 5 cm, b = 7 cm, C = 60° | c ≈ 6.24 cm |
| 2 | a = 8 cm, b = 10 cm, c = 12 cm | C ≈ 82.8° |
| 3 | a = 3 cm, b = 4 cm, C = 120° | c ≈ 6.08 cm or c ≈ 8.06 cm |
As we’ve worked through these problems, you’ve seen how the Law of Cosines can be used to find the length of the third side of a triangle, as well as the angle between two sides. Remember to always check for ambiguous cases, as there may be multiple possible solutions.
By applying the Law of Cosines, you can solve a wide range of problems involving triangles. With practice, you’ll become more comfortable and proficient in using this powerful tool in trigonometry.
In the next section, we’ll explore some frequently asked questions related to the Law of Cosines.
What is the Law of Cosines used for?
+The Law of Cosines is used to find the length of the third side of a triangle when you know the lengths of the other two sides and the angle between them.
Can the Law of Cosines be used to find the angle between two sides?
+Yes, the Law of Cosines can be rearranged to solve for the angle between two sides, given the lengths of all three sides.
What is an ambiguous case in the Law of Cosines?
+An ambiguous case occurs when there are two possible solutions for the length of the third side, often due to the angle between the two known sides being greater than 90°.
Related Terms:
- Law of Sines worksheet
- Law of Sines Worksheet pdf
- Law of Cosines Notes
- Law of Cosines Quiz