Kepler's 3 Laws of Planetary Motion Worksheet Answers

Understanding Kepler's 3 Laws of Planetary Motion
In the early 17th century, Johannes Kepler, a German mathematician and astronomer, discovered three fundamental laws that describe the motion of planets around the Sun. These laws, known as Kepler’s Laws of Planetary Motion, revolutionized our understanding of the solar system and paved the way for Sir Isaac Newton’s law of universal gravitation.
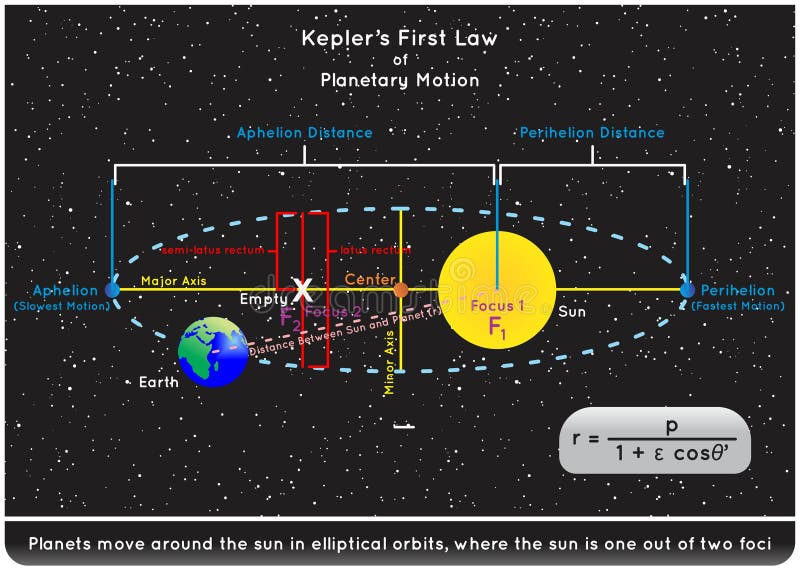
Kepler's First Law: The Law of Ellipses
Kepler’s First Law states that the orbits of the planets are elliptical in shape, with the Sun at one of the two foci. This means that the distance between the planet and the Sun varies throughout the year, with the closest point called perihelion and the farthest point called aphelion.
| Term | Definition |
|---|---|
| Perihelion | The point in a planet's orbit when it is closest to the Sun |
| Aphelion | The point in a planet's orbit when it is farthest from the Sun |
| Eccentricity | A measure of the elliptical shape of a planet's orbit |
Kepler's Second Law: The Law of Equal Areas
Kepler’s Second Law states that the line connecting the planet to the Sun sweeps out equal areas in equal times. This means that the planet moves faster when it is closer to the Sun and slower when it is farther away.
🌟 Note: This law implies that the planet's speed is not constant, but rather varies as it orbits the Sun.
Kepler's Third Law: The Law of Harmonies
Kepler’s Third Law states that the square of a planet’s orbital period is proportional to the cube of its semi-major axis. This law allows us to calculate the orbital period of a planet if we know its distance from the Sun.
🔍 Note: The semi-major axis is the average distance of a planet from the Sun, and the orbital period is the time it takes for the planet to complete one orbit.
Worksheet Answers
- What is the shape of a planet’s orbit according to Kepler’s First Law? Answer: Elliptical
- What is the point in a planet’s orbit when it is closest to the Sun? Answer: Perihelion
- What is the law that describes the relationship between a planet’s speed and its distance from the Sun? Answer: Kepler’s Second Law: The Law of Equal Areas
- What is the constant of proportionality in Kepler’s Third Law? Answer: The square of the orbital period is proportional to the cube of the semi-major axis
- Which law allows us to calculate the orbital period of a planet if we know its distance from the Sun? Answer: Kepler’s Third Law: The Law of Harmonies
As we can see, Kepler’s Laws of Planetary Motion provide a fundamental understanding of the solar system and the behavior of planets. These laws have been widely used in astronomy and space exploration to predict the orbits of planets, moons, and other celestial bodies.
In summary, Kepler’s Laws are a cornerstone of astronomy and have far-reaching implications for our understanding of the universe. By understanding these laws, we can gain insights into the behavior of celestial bodies and the underlying forces that govern their motion.
Related Terms:
- Kepler Second Law
- Kepler's third law diagram