Mastering Polygons: Interior Angles Made Easy
Unlocking the Secrets of Polygons: A Deep Dive into Interior Angles
Are you ready to take your geometry skills to the next level? Understanding polygons and their interior angles is a fundamental concept in mathematics, and with this guide, you’ll be able to master it in no time. In this comprehensive article, we’ll delve into the world of polygons, explore the concept of interior angles, and provide you with practical tips and tricks to make calculations a breeze.
What are Polygons?
A polygon is a two-dimensional shape with at least three sides. The word “polygon” comes from the Greek words “poly” meaning “many” and “gon” meaning “angle.” Polygons can be classified into different types based on the number of sides they have, such as triangles, quadrilaterals, pentagons, and so on.
Types of Polygons
- Triangles: A polygon with three sides.
- Quadrilaterals: A polygon with four sides.
- Pentagons: A polygon with five sides.
- Hexagons: A polygon with six sides.
- Heptagons: A polygon with seven sides.
- Octagons: A polygon with eight sides.
What are Interior Angles?
An interior angle is an angle formed by two adjacent sides of a polygon. The sum of the interior angles of a polygon is always constant and depends on the number of sides the polygon has. The formula to calculate the sum of interior angles is:
(n-2) × 180°
where n is the number of sides of the polygon.
Calculating Interior Angles
Let’s take a triangle as an example. A triangle has three sides, so n = 3.
(3-2) × 180° = 1 × 180° = 180°
This means that the sum of the interior angles of a triangle is always 180°.
For a quadrilateral, n = 4.
(4-2) × 180° = 2 × 180° = 360°
The sum of the interior angles of a quadrilateral is always 360°.
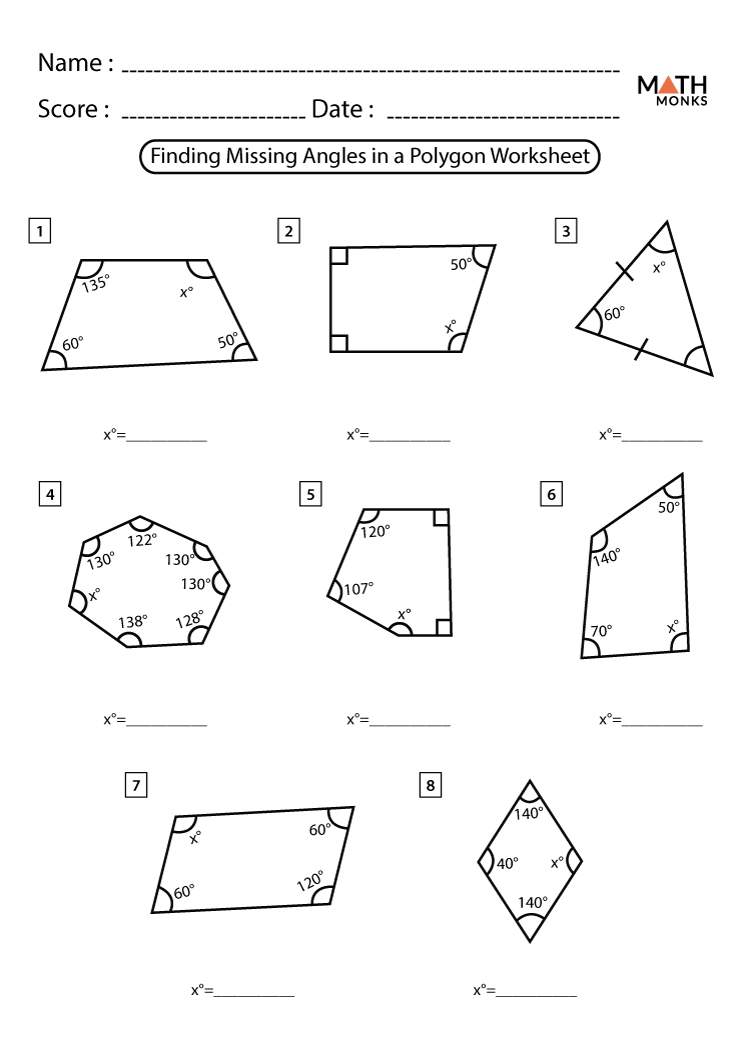
How to Calculate Interior Angles of a Polygon
Calculating interior angles of a polygon can be a straightforward process if you follow these steps:
- Determine the number of sides of the polygon (n).
- Use the formula (n-2) × 180° to calculate the sum of the interior angles.
- Divide the sum of the interior angles by the number of sides to find the measure of each interior angle.
📝 Note: This method assumes that the polygon is a regular polygon, meaning all sides and angles are equal. If the polygon is irregular, you'll need to use a different method to calculate the interior angles.
Example Problems
Let’s practice calculating interior angles with a few example problems:
- Problem 1: Find the sum of the interior angles of a hexagon.
- Solution: n = 6, so (6-2) × 180° = 4 × 180° = 720°.
- Problem 2: Find the measure of each interior angle of a regular octagon.
- Solution: n = 8, so (8-2) × 180° = 6 × 180° = 1080°. Divide by 8 to get 135° per interior angle.
Table of Sum of Interior Angles
Here’s a handy table to help you quickly find the sum of interior angles for different polygons:

| Polygon | Number of Sides (n) | Sum of Interior Angles |
|---|---|---|
| Triangle | 3 | 180° |
| Quadrilateral | 4 | 360° |
| Pentagon | 5 | 540° |
| Hexagon | 6 | 720° |
| Heptagon | 7 | 900° |
| Octagon | 8 | 1080° |
In conclusion, mastering polygons and their interior angles is a fundamental concept in mathematics. By understanding the formula (n-2) × 180° and practicing with example problems, you’ll be able to calculate interior angles with ease. Remember to use the table as a quick reference guide to help you solve problems efficiently.
What is the sum of the interior angles of a triangle?
+The sum of the interior angles of a triangle is always 180°.
How do I calculate the interior angles of a polygon?
+Use the formula (n-2) × 180°, where n is the number of sides of the polygon.
What is the measure of each interior angle of a regular octagon?
+The measure of each interior angle of a regular octagon is 135°.