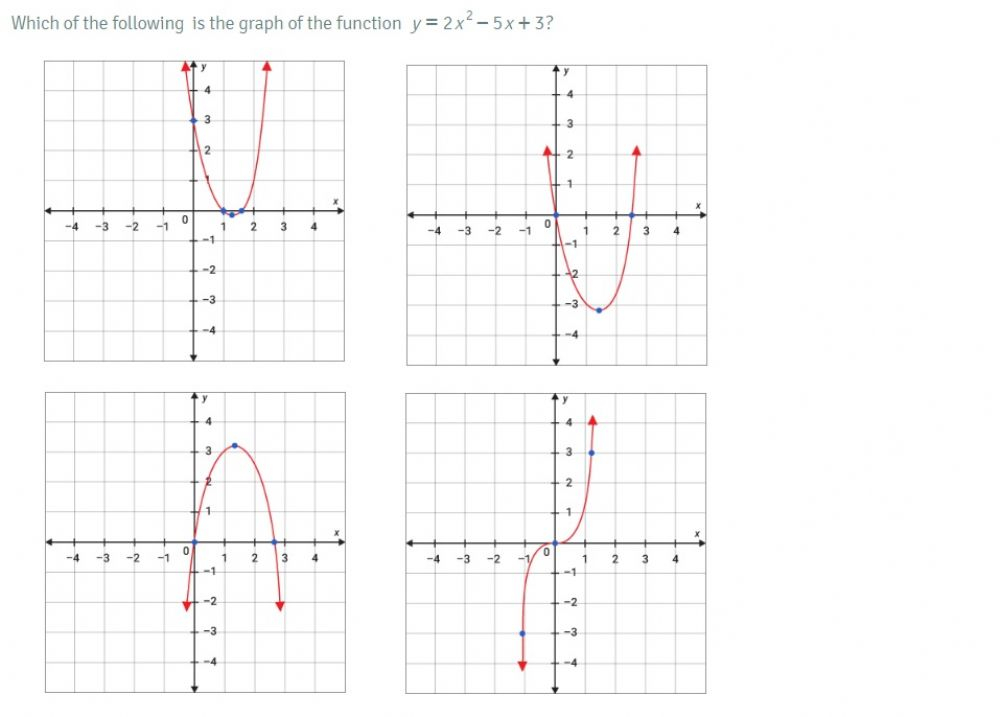
Graphing Quadratic Functions Made Easy Worksheet

Understanding Quadratic Functions
Quadratic functions are a fundamental concept in algebra and are used to model a wide range of real-world phenomena, from the trajectory of a thrown ball to the shape of a satellite dish. A quadratic function is a polynomial function of degree two, which means the highest power of the variable is two. The general form of a quadratic function is f(x) = ax^2 + bx + c, where a, b, and c are constants.
The Anatomy of a Quadratic Function
Before we dive into graphing quadratic functions, it’s essential to understand the different parts of the function.
- a: The coefficient of the x^2 term, which determines the direction and width of the parabola. If a is positive, the parabola opens upward; if a is negative, it opens downward.
- b: The coefficient of the x term, which determines the position of the parabola along the x-axis.
- c: The constant term, which determines the position of the parabola along the y-axis.
Graphing Quadratic Functions
Now that we’ve covered the basics, let’s move on to graphing quadratic functions. There are several ways to graph a quadratic function, but we’ll focus on the most common method: using the vertex form.
Vertex Form
The vertex form of a quadratic function is f(x) = a(x - h)^2 + k, where (h, k) is the vertex of the parabola. To graph a quadratic function in vertex form, follow these steps:
- Identify the vertex (h, k) from the equation.
- Plot the vertex on the coordinate plane.
- Determine the direction of the parabola based on the value of a. If a is positive, the parabola opens upward; if a is negative, it opens downward.
- Plot two additional points on either side of the vertex, using the fact that the parabola is symmetric about the vertical line x = h.
- Connect the three points with a smooth curve.
Example
Graph the quadratic function f(x) = (x - 2)^2 + 3.
- Identify the vertex (2, 3) from the equation.
- Plot the vertex on the coordinate plane.
- Determine the direction of the parabola. Since a is positive (implied by the absence of a coefficient), the parabola opens upward.
- Plot two additional points on either side of the vertex, such as (1, 2) and (3, 4).
- Connect the three points with a smooth curve.
Graphing Quadratic Functions in Standard Form
While vertex form is the most common way to graph quadratic functions, you may also encounter functions in standard form: f(x) = ax^2 + bx + c. To graph a quadratic function in standard form, follow these steps:
- Determine the x-intercepts by setting f(x) = 0 and solving for x.
- Plot the x-intercepts on the coordinate plane.
- Use the x-intercepts to determine the vertex of the parabola.
- Plot the vertex on the coordinate plane.
- Determine the direction of the parabola based on the value of a. If a is positive, the parabola opens upward; if a is negative, it opens downward.
- Plot two additional points on either side of the vertex, using the fact that the parabola is symmetric about the vertical line x = h.
- Connect the three points with a smooth curve.
Example
Graph the quadratic function f(x) = x^2 + 4x + 4.
- Determine the x-intercepts by setting f(x) = 0 and solving for x. The x-intercepts are (-2, 0).
- Plot the x-intercepts on the coordinate plane.
- Use the x-intercepts to determine the vertex of the parabola. The vertex is (-2, -4).
- Plot the vertex on the coordinate plane.
- Determine the direction of the parabola. Since a is positive, the parabola opens upward.
- Plot two additional points on either side of the vertex, such as (-3, -5) and (-1, -3).
- Connect the three points with a smooth curve.
Common Graphs of Quadratic Functions
Here are some common graphs of quadratic functions:
| Type of Graph | Equation | Description |
|---|---|---|
| Upward-opening parabola | f(x) = x^2 | The graph opens upward, with a vertex at (0, 0). |
| Downward-opening parabola | f(x) = -x^2 | The graph opens downward, with a vertex at (0, 0). |
| Horizontal shift | f(x) = (x - h)^2 | The graph is shifted horizontally by h units. |
| Vertical shift | f(x) = x^2 + k | The graph is shifted vertically by k units. |
| Compressed graph | f(x) = ax^2, where a > 1 | The graph is compressed vertically. |
| Stretched graph | f(x) = ax^2, where 0 < a < 1 | The graph is stretched vertically. |
📝 Note: These are just a few examples of common graphs of quadratic functions. By combining different transformations, you can create a wide range of graphs.
To practice graphing quadratic functions, try the following exercises:
Practice Exercises
Graph the following quadratic functions:
- f(x) = x^2 + 2x + 1
- f(x) = (x - 1)^2 - 2
- f(x) = -x^2 + 4x - 3
Now that you’ve mastered the basics of graphing quadratic functions, you’re ready to move on to more advanced topics in algebra.
Until next time, happy graphing!
What is the vertex form of a quadratic function?
+The vertex form of a quadratic function is f(x) = a(x - h)^2 + k, where (h, k) is the vertex of the parabola.
How do I graph a quadratic function in standard form?
+To graph a quadratic function in standard form, determine the x-intercepts, plot the vertex, and determine the direction of the parabola based on the value of a.
What is the difference between a upward-opening and downward-opening parabola?
+An upward-opening parabola has a positive value of a, while a downward-opening parabola has a negative value of a.