7 Ways to Master Quadratic Graphs
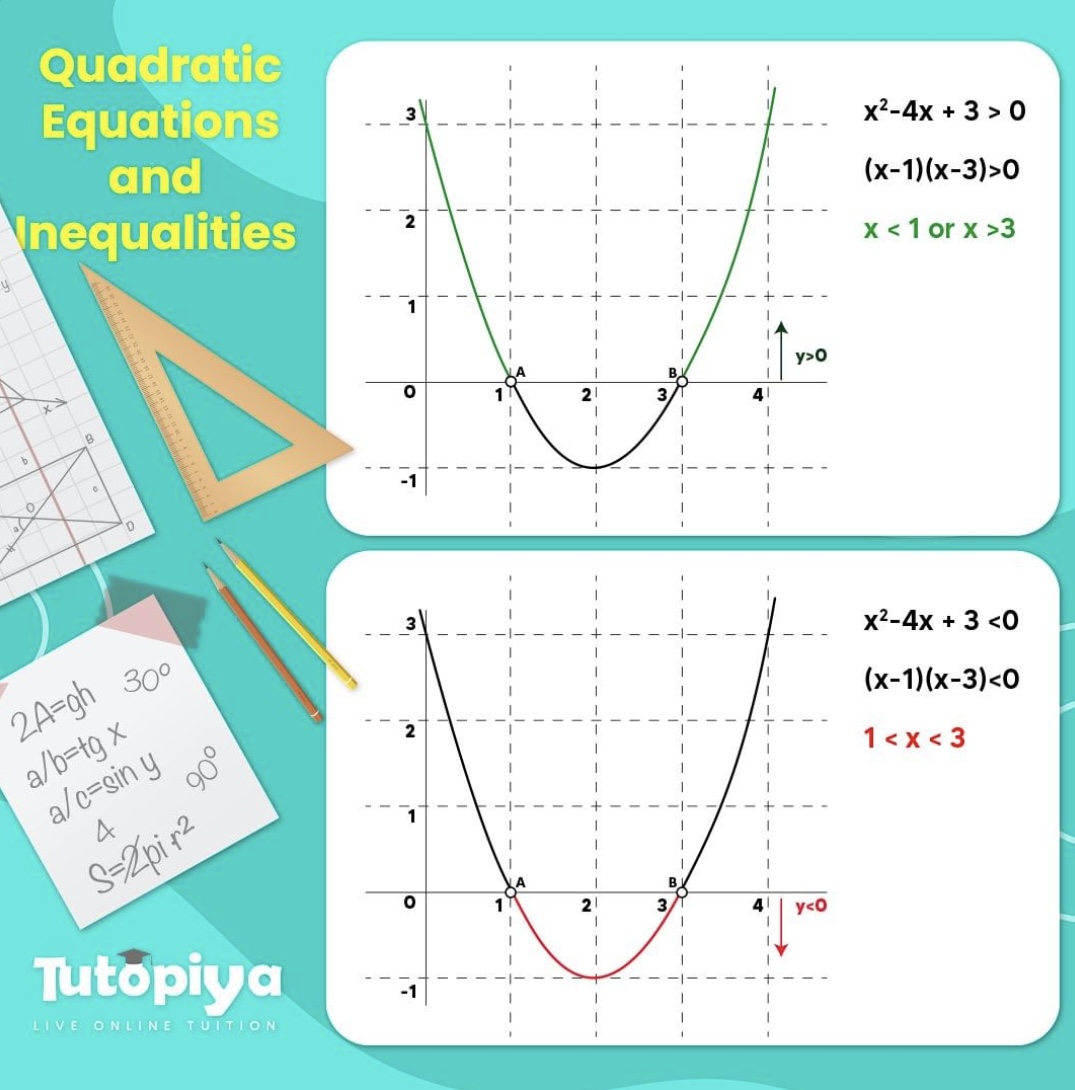
Understanding Quadratic Graphs: A Foundational Concept in Mathematics
Quadratic graphs are a fundamental concept in mathematics, and mastering them is essential for problem-solving in various fields, including physics, engineering, and economics. A quadratic graph represents a quadratic equation in the form of f(x) = ax^2 + bx + c, where ‘a’, ‘b’, and ‘c’ are constants. In this article, we will explore seven ways to master quadratic graphs, including understanding the basic concept, learning the different forms, and applying practical examples.
1. Understanding the Basic Concept of Quadratic Graphs
A quadratic graph is a parabola-shaped curve that opens upwards or downwards, depending on the value of ‘a’. The graph has a vertex, which is the lowest or highest point on the curve, and an axis of symmetry, which is the vertical line that passes through the vertex. The graph can also have x-intercepts, which are the points where the curve crosses the x-axis.
📝 Note: The vertex form of a quadratic equation is f(x) = a(x - h)^2 + k, where (h, k) is the vertex of the graph.
2. Learning the Different Forms of Quadratic Equations
There are three main forms of quadratic equations: standard form, vertex form, and factored form.
- Standard form: f(x) = ax^2 + bx + c
- Vertex form: f(x) = a(x - h)^2 + k
- Factored form: f(x) = (x - r)(x - s), where r and s are the roots of the equation
Understanding the different forms of quadratic equations is crucial for solving problems and graphing quadratic functions.
3. Understanding the Graphical Representation of Quadratic Equations
The graphical representation of a quadratic equation is a parabola-shaped curve that opens upwards or downwards. The graph can be:
- Concave upwards (a > 0)
- Concave downwards (a < 0)
- A straight line (a = 0)
The graph can also have x-intercepts, which are the points where the curve crosses the x-axis.
4. Using Quadratic Formula to Solve Equations
The quadratic formula is a powerful tool for solving quadratic equations. The formula is:
x = (-b ± √(b^2 - 4ac)) / 2a
This formula can be used to solve quadratic equations in the standard form.
📝 Note: The quadratic formula can be used to solve quadratic equations with complex roots.
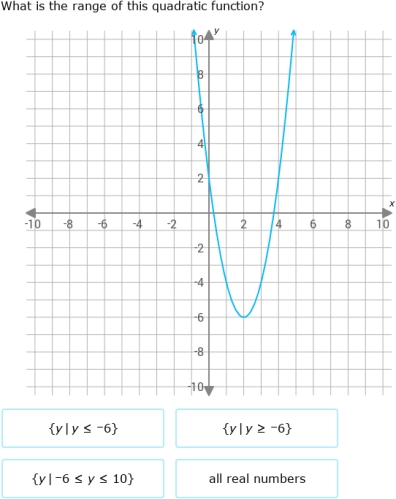
5. Graphing Quadratic Functions Using a Table of Values
Graphing a quadratic function using a table of values is a practical way to visualize the graph. To graph a quadratic function, create a table of values by substituting different values of x into the equation and calculating the corresponding values of y.
| x | y |
|---|---|
| -2 | f(-2) |
| -1 | f(-1) |
| 0 | f(0) |
| 1 | f(1) |
| 2 | f(2) |
Plot the points on a coordinate plane and join them to form a smooth curve.
6. Identifying Key Features of Quadratic Graphs
Identifying key features of quadratic graphs is essential for solving problems and graphing quadratic functions. The key features of a quadratic graph include:
- Vertex: The lowest or highest point on the curve
- Axis of symmetry: The vertical line that passes through the vertex
- X-intercepts: The points where the curve crosses the x-axis
7. Practicing with Real-World Examples
Practicing with real-world examples is an effective way to master quadratic graphs. Here are a few examples:
- A ball is thrown upwards from the ground with an initial velocity of 20 m/s. The height of the ball above the ground is given by the equation h(t) = -5t^2 + 20t + 1, where t is the time in seconds. Graph the equation and find the maximum height reached by the ball.
- A company produces a product that has a quadratic cost function C(x) = 2x^2 + 10x + 50, where x is the number of units produced. Graph the equation and find the minimum cost.
What is the difference between a quadratic equation and a quadratic graph?
+A quadratic equation is a mathematical equation in the form of ax^2 + bx + c, while a quadratic graph is the graphical representation of the equation.
How do I determine the vertex of a quadratic graph?
+The vertex of a quadratic graph can be determined using the vertex form of the equation, which is f(x) = a(x - h)^2 + k. The vertex is the point (h, k).
What is the quadratic formula, and how do I use it?
+The quadratic formula is x = (-b ± √(b^2 - 4ac)) / 2a, where a, b, and c are the coefficients of the quadratic equation. It can be used to solve quadratic equations in the standard form.
Mastering quadratic graphs requires a combination of theoretical knowledge and practical application. By understanding the basic concept, learning the different forms, and applying practical examples, you can become proficient in solving quadratic equations and graphing quadratic functions.



