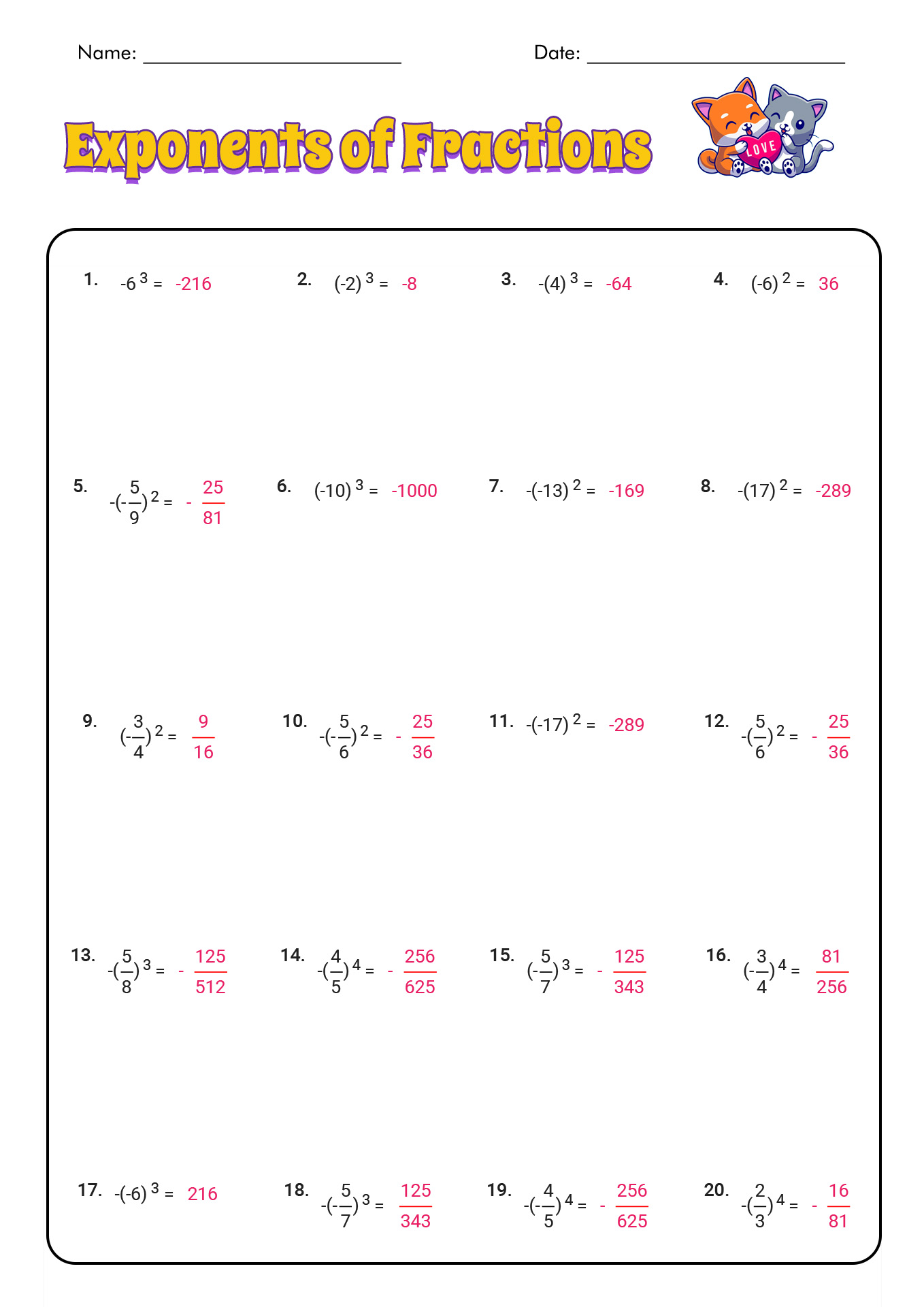
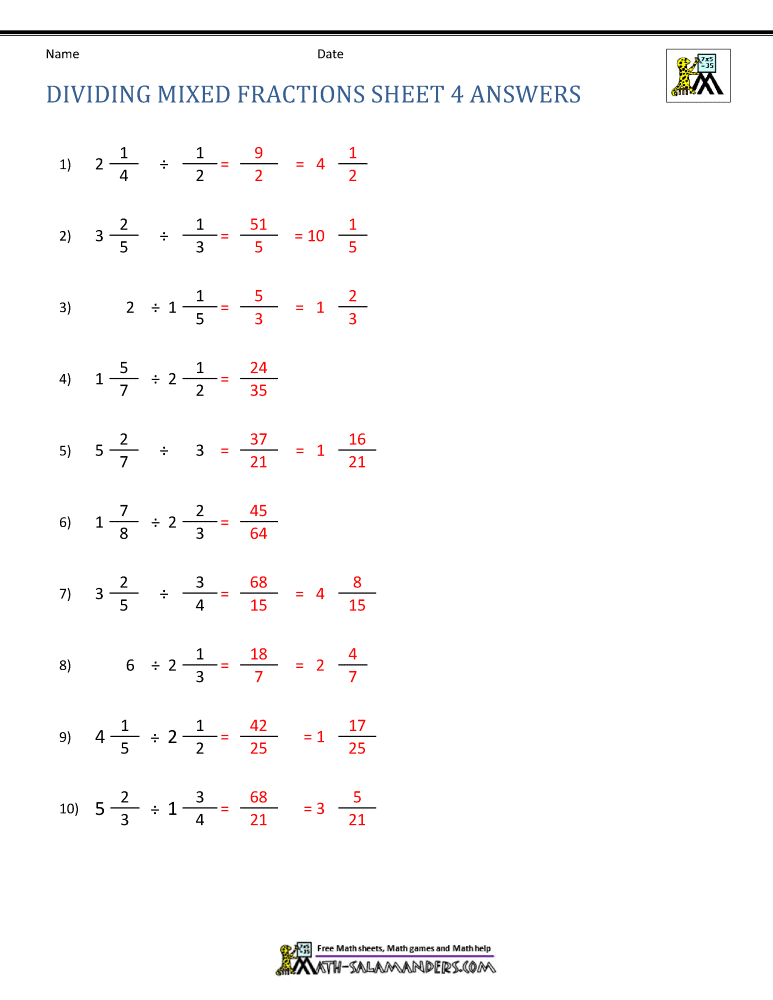5 Ways to Master Graphing Inequalities
Understanding Inequalities and Their Representation on Graphs
Graphing inequalities is a fundamental concept in algebra and mathematics, and mastering it can help you solve a wide range of problems. An inequality is a statement that compares two expressions using inequality signs such as <, >, ≤, or ≥. Graphing inequalities involves representing these statements on a coordinate plane, which helps visualize the solution set.
In this article, we will explore five ways to master graphing inequalities, including understanding the concept of inequalities, learning different types of inequalities, using test points, graphing systems of inequalities, and using technology to visualize inequalities.
1. Understanding the Concept of Inequalities
Before we dive into graphing inequalities, it’s essential to understand the concept of inequalities. An inequality is a statement that compares two expressions using inequality signs. For example, 2x + 3 > 5 is an inequality that compares the expression 2x + 3 to the value 5.
Inequalities can be categorized into different types, including:
- Linear inequalities: These inequalities have a linear expression on one side and a constant on the other side. For example, 2x + 3 > 5.
- Quadratic inequalities: These inequalities have a quadratic expression on one side and a constant on the other side. For example, x^2 + 4x + 4 > 0.
- Rational inequalities: These inequalities have a rational expression on one side and a constant on the other side. For example, (x + 1)/(x - 2) > 0.
📝 Note: Understanding the different types of inequalities is crucial for graphing them correctly.
2. Learning Different Types of Inequalities
There are different types of inequalities, and learning them is essential for graphing inequalities. Here are some of the most common types of inequalities:
- Less than (<): This inequality is represented by an open circle on the number line.
- Greater than (>): This inequality is represented by an open circle on the number line.
- Less than or equal to (≤): This inequality is represented by a closed circle on the number line.
- Greater than or equal to (≥): This inequality is represented by a closed circle on the number line.
Here is a table that summarizes the different types of inequalities:
| Inequality Sign | Representation on Number Line |
|---|---|
| < | Open circle |
| > | Open circle |
| ≤ | Closed circle |
| ≥ | Closed circle |
3. Using Test Points
Using test points is an effective way to graph inequalities. A test point is a point that is substituted into the inequality to determine whether it is true or false. Here’s how to use test points:
- Choose a point on the coordinate plane.
- Substitute the point into the inequality.
- Determine whether the inequality is true or false.
- If the inequality is true, shade the region that includes the point. If the inequality is false, shade the region that does not include the point.
📝 Note: Using test points can help you determine the direction of the inequality.
4. Graphing Systems of Inequalities
Graphing systems of inequalities involves graphing multiple inequalities on the same coordinate plane. Here’s how to graph systems of inequalities:
- Graph each inequality separately.
- Determine the region that satisfies both inequalities.
- Shade the region that satisfies both inequalities.
For example, consider the system of inequalities:
x + y > 2 x - y < 1
To graph this system, we need to graph each inequality separately and then determine the region that satisfies both inequalities.
5. Using Technology to Visualize Inequalities
Technology can be a powerful tool for visualizing inequalities. There are many online tools and software programs that can help you graph inequalities, including:
- Graphing calculators: These calculators can help you graph inequalities and visualize the solution set.
- Computer algebra systems: These systems can help you graph inequalities and solve systems of inequalities.
- Online graphing tools: These tools can help you graph inequalities and visualize the solution set.
Using technology can help you visualize inequalities and make it easier to understand the concept of inequalities.
Finally, graphing inequalities is an essential skill in mathematics, and mastering it can help you solve a wide range of problems. By understanding the concept of inequalities, learning different types of inequalities, using test points, graphing systems of inequalities, and using technology to visualize inequalities, you can become proficient in graphing inequalities.
In summary, graphing inequalities involves understanding the concept of inequalities, learning different types of inequalities, using test points, graphing systems of inequalities, and using technology to visualize inequalities. By following these steps, you can master graphing inequalities and become proficient in solving a wide range of problems.
What is an inequality?
+An inequality is a statement that compares two expressions using inequality signs such as <, >, ≤, or ≥.
How do I graph a linear inequality?
+To graph a linear inequality, use a test point to determine the direction of the inequality, and then shade the region that satisfies the inequality.
What is a system of inequalities?
+A system of inequalities is a set of multiple inequalities that must be satisfied simultaneously.