Graph Piecewise Functions Worksheet
Understanding and Graphing Piecewise Functions
Piecewise functions are mathematical functions that are defined by multiple sub-functions, each applied to a specific interval of the input value. In this article, we will explore piecewise functions, their types, and how to graph them.
What are Piecewise Functions?
A piecewise function is a function that is defined by multiple sub-functions, each applied to a specific interval of the input value. The sub-functions are typically different mathematical expressions, and the intervals are usually defined by inequalities or equalities. Piecewise functions are useful for modeling real-world situations where the behavior of a system changes suddenly at certain points.
Types of Piecewise Functions
There are several types of piecewise functions, including:
- Step function: A function that has a constant value on each interval, with a sudden jump at the endpoint of each interval.
- Absolute value function: A function that has a V-shaped graph, with the minimum value at the vertex.
- Signum function: A function that returns the sign of the input value, with a value of -1 for negative inputs, 0 for zero, and 1 for positive inputs.
- Ramp function: A function that has a linear increase or decrease on each interval, with a sudden change at the endpoint of each interval.
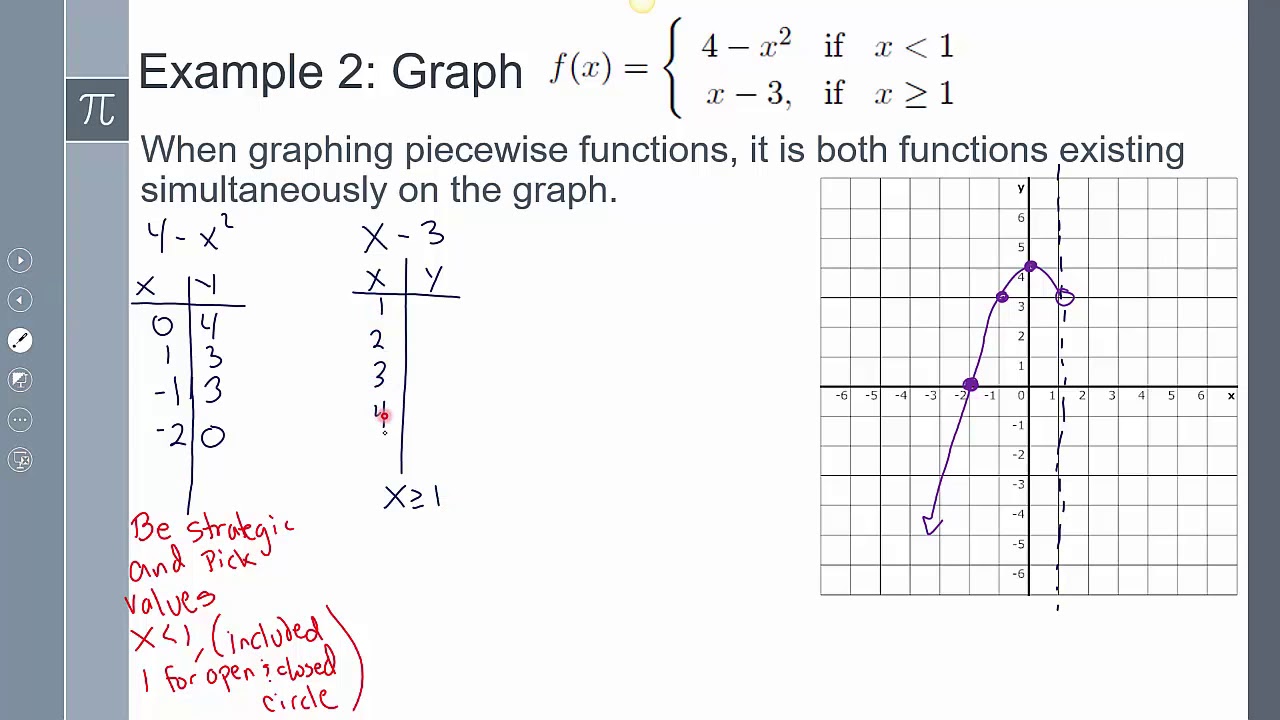
How to Graph Piecewise Functions
Graphing a piecewise function involves graphing each sub-function on its respective interval. Here are the steps to follow:
- Identify the intervals: Identify the intervals on which each sub-function is defined. These intervals are usually defined by inequalities or equalities.
- Graph each sub-function: Graph each sub-function on its respective interval. Use a different color or symbol for each sub-function to distinguish them.
- Connect the sub-functions: Connect the sub-functions at the endpoints of each interval, making sure to match the values of the sub-functions at the endpoints.
- Check for continuity: Check if the piecewise function is continuous at the endpoints of each interval. If it is not continuous, indicate the discontinuity with an open circle.
Examples of Piecewise Functions
Here are some examples of piecewise functions:
- Step function:
f(x) = { 0, x < 0 { 1, x ≥ 0 }
This function has a constant value of 0 on the interval x < 0 and a constant value of 1 on the interval x ≥ 0.
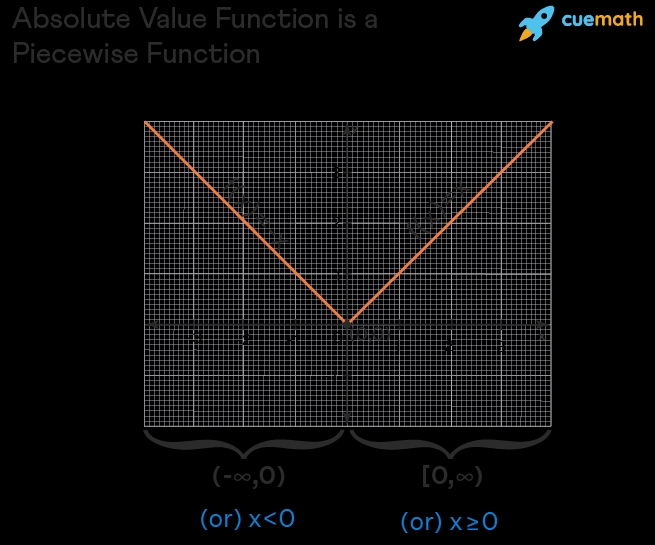
- Absolute value function:
f(x) = |x|
This function has a V-shaped graph, with the minimum value at the vertex x = 0.
- Signum function:
f(x) = sgn(x) = { -1, x < 0 { 0, x = 0 { 1, x > 0 }
This function returns the sign of the input value, with a value of -1 for negative inputs, 0 for zero, and 1 for positive inputs.
Graphing Piecewise Functions with Tables
Sometimes, it is helpful to use a table to graph a piecewise function. Here is an example:
| x | f(x) |
|---|---|
| -2 | 0 |
| -1 | 0 |
| 0 | 1 |
| 1 | 1 |
| 2 | 1 |
This table represents the step function f(x) = { 0, x < 0; 1, x ≥ 0 }.
Common Mistakes when Graphing Piecewise Functions
Here are some common mistakes to avoid when graphing piecewise functions:
- Forgetting to connect the sub-functions: Make sure to connect the sub-functions at the endpoints of each interval.
- Not checking for continuity: Check if the piecewise function is continuous at the endpoints of each interval.
- Not using different colors or symbols: Use different colors or symbols for each sub-function to distinguish them.
📝 Note: When graphing piecewise functions, make sure to check for continuity at the endpoints of each interval.
What is a piecewise function?
+A piecewise function is a function that is defined by multiple sub-functions, each applied to a specific interval of the input value.
How do I graph a piecewise function?
+Graph each sub-function on its respective interval, connect the sub-functions at the endpoints of each interval, and check for continuity.
What are some common mistakes to avoid when graphing piecewise functions?
+Forgetting to connect the sub-functions, not checking for continuity, and not using different colors or symbols for each sub-function.
In conclusion, graphing piecewise functions requires attention to detail and a clear understanding of the intervals on which each sub-function is defined. By following the steps outlined above and avoiding common mistakes, you can create accurate graphs of piecewise functions.
Related Terms:
- Piecewise Functions Worksheet Word Problems
- Evaluating piecewise Functions worksheet
- Writing piecewise Functions worksheet
- Evaluating piecewise Functions Worksheet pdf
- Linear piecewise Functions worksheet