5 Ways to Master Geometry Transformations
Geometry transformations are a fundamental concept in mathematics and computer graphics. Understanding how to master these transformations can help you in various fields, such as graphic design, engineering, and architecture. In this article, we will explore five ways to master geometry transformations and provide examples and tips to help you improve your skills.
1. Understanding the Basics of Geometry Transformations
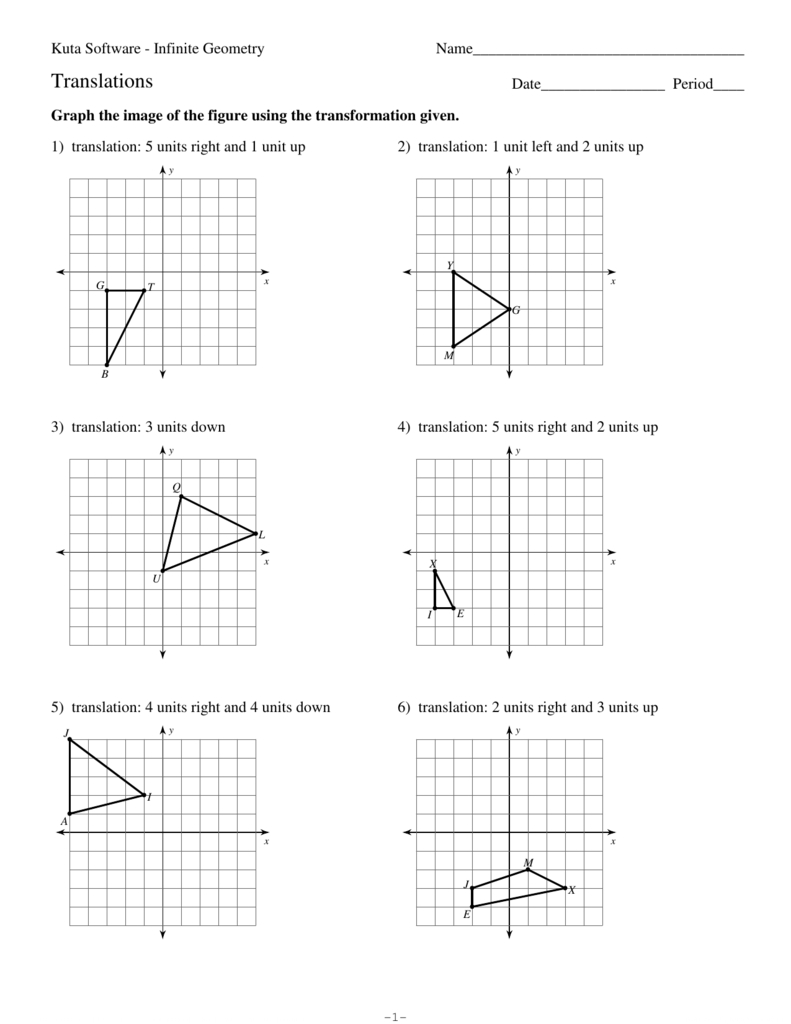
To master geometry transformations, it’s essential to understand the basics of translation, rotation, scaling, and reflection. These four transformations are the building blocks of more complex transformations.
- Translation: Moving an object from one position to another without changing its size or orientation.
- Rotation: Rotating an object around a fixed point without changing its size or shape.
- Scaling: Changing the size of an object without changing its shape or orientation.
- Reflection: Flipping an object over a line or plane without changing its size or shape.
Understanding these basic transformations will help you to create more complex transformations and apply them to real-world problems.
2. Using Matrices to Represent Transformations
Matrices are a powerful tool for representing and combining transformations. A matrix is a table of numbers that can be used to perform transformations on objects. By multiplying a matrix by a vector, you can apply a transformation to the vector.
For example, the following matrix represents a translation of 2 units in the x-direction and 3 units in the y-direction:
[1 0 2]
[0 1 3]
[0 0 1]
By multiplying this matrix by a vector, you can apply the translation to the vector.
Example:
Suppose we want to translate a point (x, y) = (4, 5) by 2 units in the x-direction and 3 units in the y-direction. We can represent the point as a vector (4, 5, 1) and multiply it by the translation matrix:
[1 0 2] [4] [6]
[0 1 3] [5] = [8]
[0 0 1] [1] [1]
The resulting vector (6, 8, 1) represents the translated point.
3. Practicing with Interactive Tools
Interactive tools, such as GeoGebra or Mathematica, can help you to visualize and practice geometry transformations. These tools allow you to create and manipulate geometric objects, apply transformations, and explore the effects of different transformations.
Example:
Using GeoGebra, you can create a triangle and apply a rotation transformation to it. By adjusting the angle of rotation, you can see how the triangle changes.
📝 Note: Practice is key to mastering geometry transformations. Use interactive tools to experiment with different transformations and explore their effects.
4. Learning from Real-World Examples
Real-world examples can help you to understand the practical applications of geometry transformations. By studying how transformations are used in different fields, you can gain a deeper understanding of the concepts and develop your problem-solving skills.
Example:
In computer graphics, transformations are used to create animations and special effects. By applying transformations to objects, you can create the illusion of movement and depth.
Example:
In architecture, transformations are used to design and visualize buildings. By applying transformations to 2D and 3D models, architects can explore different design options and create complex shapes.
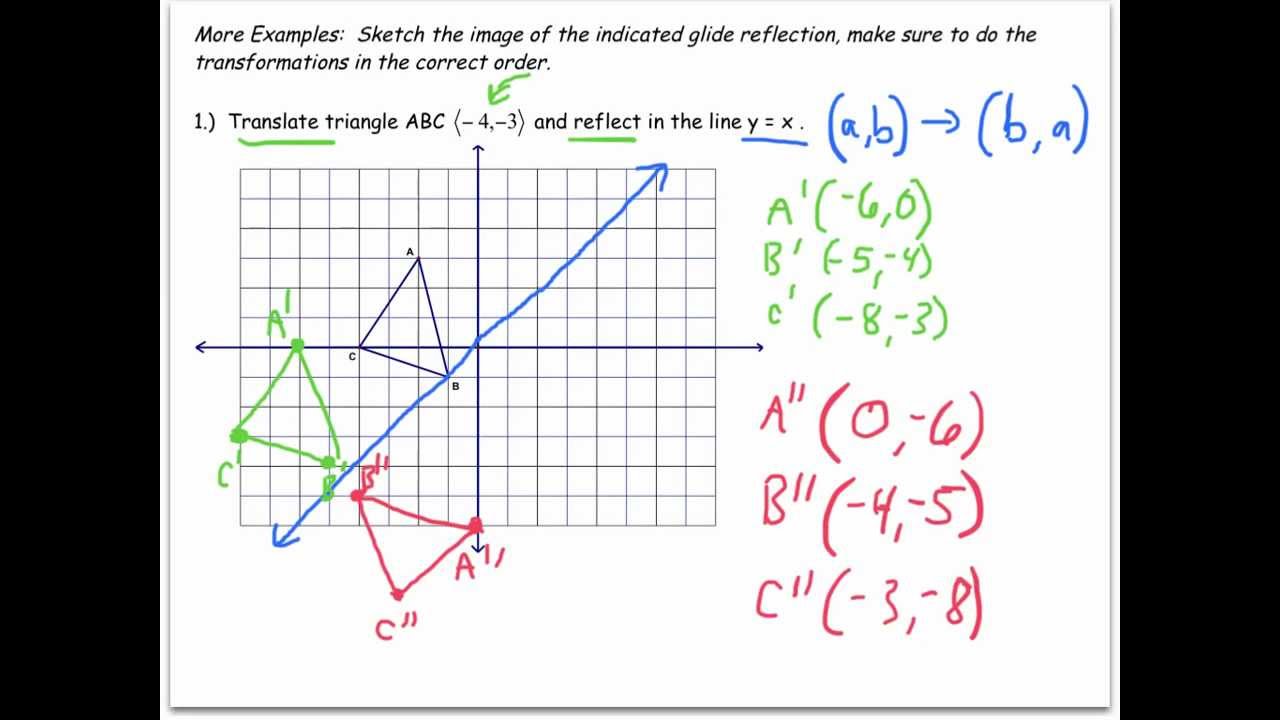
5. Breaking Down Complex Transformations
Complex transformations can be broken down into simpler transformations. By decomposing a complex transformation into its constituent parts, you can understand the individual transformations and apply them to solve problems.
Example:
Suppose we want to apply a transformation that combines a rotation, scaling, and translation. We can break down the transformation into its individual components and apply them in sequence.
📝 Note: Breaking down complex transformations can help you to understand the individual transformations and apply them to solve problems.
In conclusion, mastering geometry transformations requires a combination of understanding the basics, using matrices to represent transformations, practicing with interactive tools, learning from real-world examples, and breaking down complex transformations. By following these tips and practicing regularly, you can develop your skills and apply geometry transformations to solve problems in various fields.
What is the difference between a translation and a rotation?
+
A translation moves an object from one position to another without changing its size or orientation, while a rotation rotates an object around a fixed point without changing its size or shape.
How do I represent a transformation using a matrix?
+
A matrix can be used to represent a transformation by multiplying the matrix by a vector. The resulting vector represents the transformed point.
What are some real-world examples of geometry transformations?
+
Geometry transformations are used in computer graphics, architecture, engineering, and other fields. For example, transformations are used to create animations and special effects in movies and video games.
Related Terms:
- Geometry Transformation Composition Worksheet pdf
- Composition of transformations Worksheet Kuta