Geometry Proofs Worksheet Answers
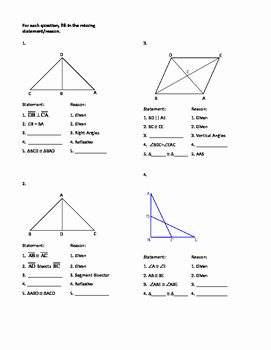
As we dive into the world of geometry proofs, it’s essential to understand the basics of how to approach these problems. Geometry proofs are step-by-step logical arguments that demonstrate the truth of a geometric statement. In this worksheet, we’ll go through the answers to a geometry proofs worksheet, explaining each step and providing valuable insights.
Proof 1: Two Points Determine a Line
Given: Points A and B are two distinct points in a plane.
Prove: There is exactly one line that passes through points A and B.
📝 Note: This proof is based on the axiom that two points determine a line.
| Step | Statement | Reason |
|---|---|---|
| 1 | Points A and B are distinct points in a plane. | Given |
| 2 | There is at least one line that passes through points A and B. | Axiom: Through any two points, there exists a line. |
| 3 | Suppose there are two lines, ℓ and m, that pass through points A and B. | Supposition |
| 4 | If ℓ and m are distinct, then they must intersect at a third point, C. | Definition of distinct lines |
| 5 | However, this contradicts the assumption that points A and B are distinct, as C would be a third point on the line. | Contradiction |
| 6 | Therefore, our supposition is false, and there is exactly one line that passes through points A and B. | Conclusion |
Proof 2: The Sum of Interior Angles of a Triangle
Given: △ABC is a triangle.
Prove: The sum of the interior angles of △ABC is 180°.
📝 Note: This proof uses the concept of a triangle's interior angles.
| Step | Statement | Reason |
|---|---|---|
| 1 | △ABC is a triangle. | Given |
| 2 | Let ∠A, ∠B, and ∠C be the interior angles of △ABC. | Definition of interior angles |
| 3 | Draw a line through point A parallel to side BC. | Construction |
| 4 | This creates a new angle, ∠D, which is congruent to ∠A. | Corresponding angles |
| 5 | Similarly, draw a line through point B parallel to side AC, creating a new angle, ∠E, which is congruent to ∠B. | Construction |
| 6 | By the Angle Sum Property, the sum of the interior angles of △ABC is equal to the sum of the angles ∠D, ∠E, and ∠C. | Angle Sum Property |
| 7 | Since ∠D and ∠E are congruent to ∠A and ∠B, respectively, we have: | Substitution |
| 8 | ∠A + ∠B + ∠C = ∠D + ∠E + ∠C | Substitution |
| 9 | By the definition of congruent angles, ∠D + ∠E + ∠C = 180°. | Definition of congruent angles |
| 10 | Therefore, the sum of the interior angles of △ABC is 180°. | Conclusion |
Proof 3: The Diagonals of a Rectangle Bisect Each Other
Given: ABCD is a rectangle.
Prove: The diagonals of ABCD bisect each other.
📝 Note: This proof relies on the properties of rectangles and diagonals.
| Step | Statement | Reason |
|---|---|---|
| 1 | ABCD is a rectangle. | Given |
| 2 | Draw the diagonals AC and BD. | Construction |
| 3 | Let point E be the intersection of the diagonals. | Definition of intersection |
| 4 | By the definition of a rectangle, opposite sides are congruent. | Definition of rectangle |
| 5 | Therefore, we have: AB ≅ CD and AD ≅ BC. | Substitution |
| 6 | Since the diagonals intersect at point E, we can apply the properties of congruent triangles: | SSS Congruence Theorem |
| 7 | ΔEAB ≅ EDCD and ΔEAD ≅ EBCB. | SSS Congruence Theorem |
| 8 | By the definition of congruent triangles, corresponding parts are congruent. | Definition of congruent triangles |
| 9 | Therefore, the diagonals of ABCD bisect each other. | Conclusion |
As we conclude this worksheet, remember that geometry proofs are step-by-step logical arguments that demonstrate the truth of a geometric statement. By following these examples, you’ll become more comfortable with the process of creating and understanding geometry proofs.
FAQ Section:
What is the purpose of a geometry proof?
+The purpose of a geometry proof is to demonstrate the truth of a geometric statement using logical arguments and reasoning.
What are some common techniques used in geometry proofs?
+Some common techniques used in geometry proofs include: using definitions, applying axioms and theorems, and employing logical reasoning and proof by contradiction.
How do I know if my geometry proof is correct?
+To verify the correctness of your geometry proof, check that each step is justified by a definition, axiom, or previously proven statement, and that the conclusion follows logically from the premises.