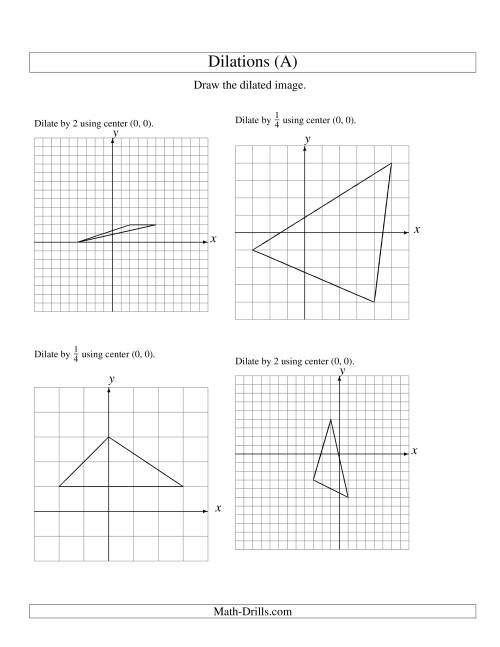
Geometry Dilations Worksheet Exercises and Answers
Understanding Geometry Dilations
Geometry dilations are a fundamental concept in mathematics, particularly in geometry and trigonometry. A dilation is a transformation that changes the size of a figure, but not its shape. In this worksheet, we will explore the concept of dilations, including the definition, types, and how to perform dilations.
Definition of a Dilation
A dilation is a transformation that enlarges or reduces a figure by a scale factor with respect to a fixed point called the center of dilation. The scale factor is a ratio of the lengths of the corresponding sides of the image and the preimage.
📝 Note: The scale factor can be greater than 1 (enlargement) or less than 1 (reduction).
Types of Dilations
There are two types of dilations:
- Enlargement: A dilation with a scale factor greater than 1, which increases the size of the figure.
- Reduction: A dilation with a scale factor less than 1, which decreases the size of the figure.
How to Perform a Dilation
To perform a dilation, follow these steps:
- Identify the center of dilation.
- Determine the scale factor.
- Multiply the coordinates of the preimage by the scale factor to obtain the coordinates of the image.
| Preimage Coordinates | Scale Factor | Image Coordinates |
|---|---|---|
| (x, y) | k | (kx, ky) |
Exercises
Perform the following dilations:
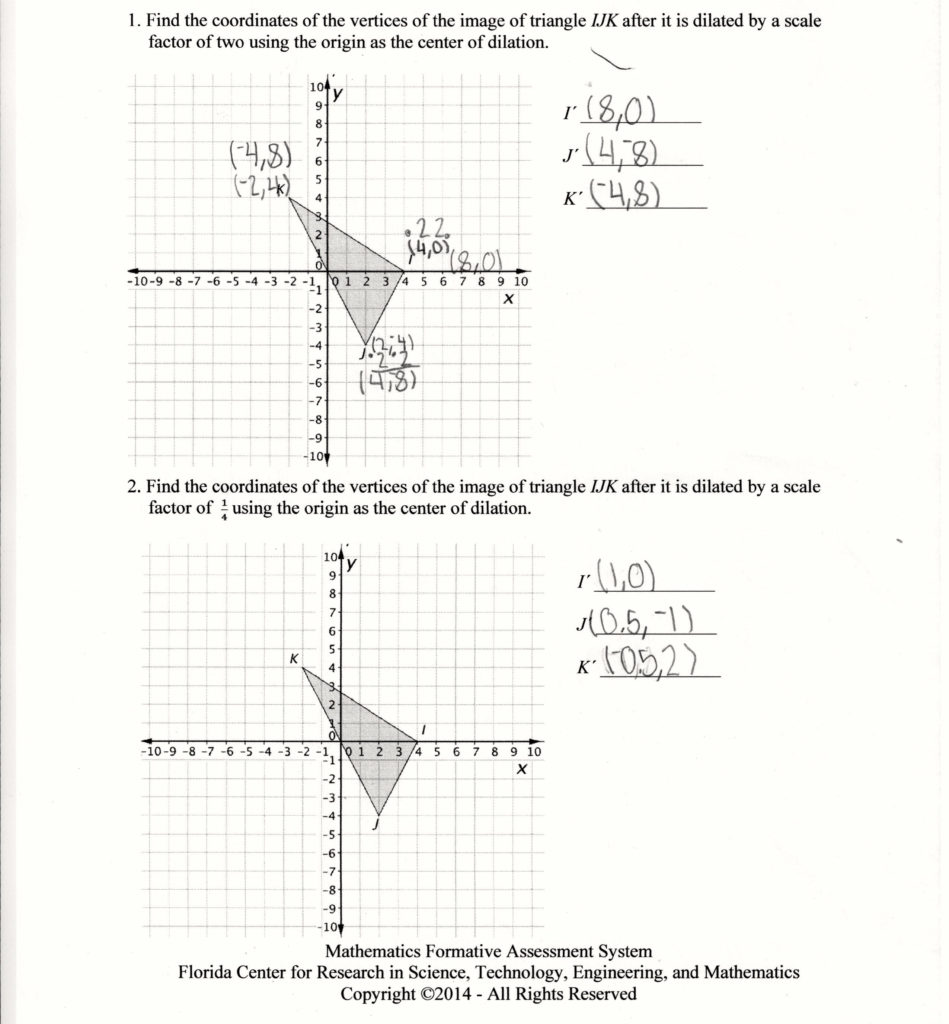
- Dilate the triangle with vertices A(2, 3), B(4, 5), and C(6, 7) by a scale factor of 2 with respect to the origin.
- Dilate the circle with center (3, 4) and radius 5 by a scale factor of 1⁄2 with respect to the point (2, 3).
- Dilate the quadrilateral with vertices W(1, 2), X(3, 4), Y(5, 6), and Z(7, 8) by a scale factor of 3⁄2 with respect to the point (2, 3).
Answers
- The image of the triangle is a triangle with vertices A’(4, 6), B’(8, 10), and C’(12, 14).
- The image of the circle is a circle with center (3⁄2, 2) and radius 5⁄2.
- The image of the quadrilateral is a quadrilateral with vertices W’(3⁄2, 3), X’(9⁄2, 6), Y’(15⁄2, 9), and Z’(21⁄2, 12).
Conclusion
In this worksheet, we have explored the concept of geometry dilations, including the definition, types, and how to perform dilations. We have also practiced performing dilations on various shapes, including triangles, circles, and quadrilaterals. By understanding dilations, you can apply this concept to various problems in geometry and trigonometry.
What is the difference between an enlargement and a reduction?
+An enlargement is a dilation with a scale factor greater than 1, which increases the size of the figure. A reduction is a dilation with a scale factor less than 1, which decreases the size of the figure.
How do you determine the center of dilation?
+The center of dilation is a fixed point that remains unchanged after the dilation. It is usually given in the problem or can be found using the coordinates of the preimage and image.
What is the formula for performing a dilation?
+The formula for performing a dilation is (kx, ky), where (x, y) are the coordinates of the preimage, k is the scale factor, and (kx, ky) are the coordinates of the image.