5 Ways to Master Function Notation
Understanding Function Notation: A Comprehensive Guide
Function notation is a fundamental concept in mathematics, particularly in algebra and calculus. It provides a concise way to express relationships between variables and represents a crucial building block for more advanced mathematical concepts. Mastering function notation can seem daunting at first, but with practice and persistence, you can become proficient in using it to solve complex problems.
What is Function Notation?
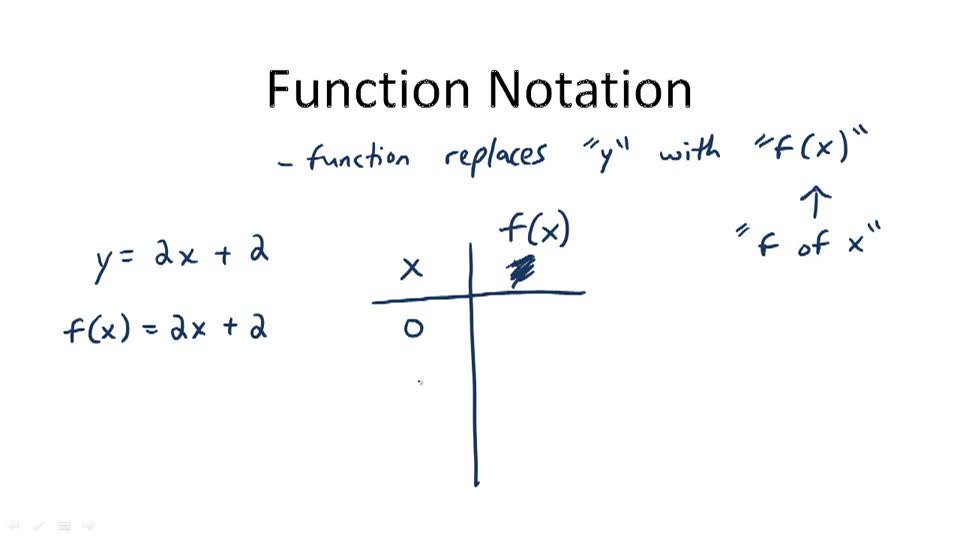
Function notation is a mathematical notation that describes the relationship between a function and its input values. It typically takes the form of f(x), where f represents the function name, and x represents the input value. The function notation is read as “f of x,” and it represents the output value of the function for the given input value.
Why is Function Notation Important?
Function notation is essential in mathematics because it:
- Provides a concise way to express complex relationships between variables
- Allows for the representation of multiple functions using a single notation
- Facilitates the composition of functions, which is crucial in calculus and other advanced mathematical concepts
- Enhances readability and clarity in mathematical expressions
5 Ways to Master Function Notation
Mastering function notation requires practice, patience, and a deep understanding of the underlying mathematical concepts. Here are five ways to help you master function notation:
1. Understand the Basics
Start by understanding the basic syntax of function notation. Familiarize yourself with the following:
- Function name: The name of the function, usually represented by a letter (e.g., f, g, h)
- Input value: The value that is input into the function, usually represented by a variable (e.g., x, y, z)
- Output value: The result of the function, usually represented by a variable (e.g., y, w, v)
For example, in the function notation f(x), “f” is the function name, and “x” is the input value.
2. Practice, Practice, Practice
Practice is key to mastering function notation. Start with simple functions, such as linear equations, and gradually move on to more complex functions, such as quadratic equations and trigonometric functions.
- Evaluate functions for different input values
- Graph functions to visualize their behavior
- Solve equations involving functions
For example, evaluate the function f(x) = 2x + 3 for x = 2, 4, and 6.

| Input Value | Output Value |
|---|---|
| 2 | 7 |
| 4 | 11 |
| 6 | 15 |
3. Learn to Simplify Functions
Simplifying functions is an essential skill in mastering function notation. Learn to simplify functions by:
- Combining like terms
- Factoring out common factors
- Canceling out common factors
For example, simplify the function f(x) = (2x + 4) / 2.
f(x) = (2x + 4) / 2 = x + 2
4. Understand Function Composition
Function composition is a critical concept in calculus and other advanced mathematical concepts. Understand how to compose functions by:
- Evaluating the inner function first
- Using the output value of the inner function as the input value of the outer function
For example, find the composition of the functions f(x) = 2x and g(x) = x^2.
(f ∘ g)(x) = f(g(x)) = f(x^2) = 2x^2
5. Use Online Resources and Practice Tools
There are many online resources and practice tools available to help you master function notation. Use these resources to:
- Practice evaluating functions
- Simplify functions
- Visualize function behavior
Some popular online resources include:
- Khan Academy
- Wolfram Alpha
- Mathway
By following these five ways to master function notation, you’ll become proficient in using function notation to solve complex problems and unlock more advanced mathematical concepts.
In conclusion, mastering function notation is a fundamental skill in mathematics that requires practice, patience, and persistence. By understanding the basics, practicing regularly, simplifying functions, understanding function composition, and using online resources and practice tools, you’ll be well on your way to becoming proficient in function notation.
What is the difference between a function and an equation?
+A function is a relation between a set of inputs and a set of possible outputs, while an equation is a statement that expresses the equality of two mathematical expressions.
How do I evaluate a function for a given input value?
+To evaluate a function for a given input value, substitute the input value into the function and simplify the resulting expression.
What is the purpose of function composition?
+Function composition is used to create new functions by combining existing functions.
Related Terms:
- Evaluating function notation Worksheet pdf
- Linear function notation worksheet
- Function Notation Worksheet pdf Kuta
- Function Notation Worksheet Algebra 2