5 Ways to Factor Trinomials Easily

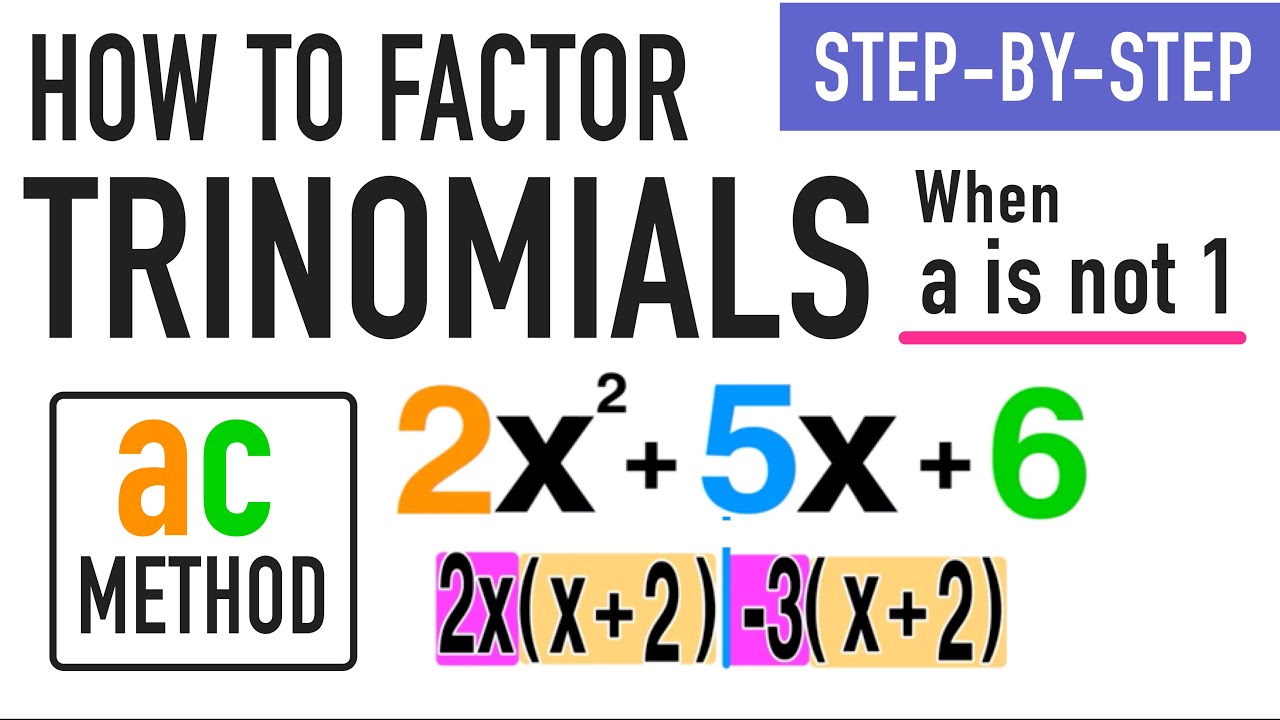
Understanding Trinomials and Factoring

When it comes to algebra, one of the most important concepts to grasp is factoring trinomials. A trinomial is a type of polynomial that consists of three terms, usually in the form of ax^2 + bx + c. Factoring trinomials involves expressing them as the product of two binomials, which can be a challenging task for many students. However, with the right strategies and techniques, factoring trinomials can be made easier.

Method 1: The FOIL Method

The FOIL method is a popular technique for factoring trinomials. FOIL stands for “First, Outer, Inner, Last,” which refers to the order in which you multiply the terms. Here’s how it works:

• Multiply the first terms of each binomial (a and d)
• Multiply the outer terms (a and c)
• Multiply the inner terms (b and d)
• Multiply the last terms (b and c)
• Add up the products and combine like terms

For example, let’s factor the trinomial x^2 + 5x + 6 using the FOIL method:

• Multiply the first terms: x*x = x^2
• Multiply the outer terms: x*6 = 6x
• Multiply the inner terms: 5x*x = 5x^2
• Multiply the last terms: 5x*6 = 30x
• Add up the products and combine like terms: x^2 + 6x + 5x + 30x = x^2 + 11x + 30x

However, this is not the correct factorization. Let’s try again:

• Multiply the first terms: x*x = x^2
• Multiply the outer terms: x*6 = 6x
• Multiply the inner terms: 5x*1 = 5x
• Multiply the last terms: 5x*1 = 5x
• Add up the products and combine like terms: x^2 + 6x + 5x = x^2 + 11x (not equal to the original trinomial)

It seems that the FOIL method does not work for this example. This is because the FOIL method only works when the trinomial can be factored into two binomials with integer coefficients.

Method 2: The AC Method

The AC method is another technique for factoring trinomials. This method involves multiplying the first and last terms of the trinomial (a and c) to get the product ac, and then finding two numbers whose product is ac and whose sum is b.

For example, let’s factor the trinomial x^2 + 5x + 6 using the AC method:

• Multiply the first and last terms: x^2*6 = 6x^2
• Find two numbers whose product is 6x^2 and whose sum is 5x: 2x and 3x
• Rewrite the trinomial using these numbers: x^2 + 2x + 3x + 6
• Factor the trinomial by grouping: (x^2 + 2x) + (3x + 6) = x(x+2) + 3(x+2) = (x+2)(x+3)

🔍 Note: The AC method is a more general method than the FOIL method and can be used to factor more types of trinomials.

Method 3: Factoring by Grouping

Factoring by grouping involves grouping the terms of the trinomial into two pairs and then factoring out a common factor from each pair.

For example, let’s factor the trinomial x^2 + 5x + 6 using factoring by grouping:

• Group the terms: (x^2 + 2x) + (3x + 6)
• Factor out a common factor from each pair: x(x+2) + 3(x+2)
• Factor out the common binomial factor: (x+2)(x+3)

Method 4: Using the Trinomial Formula

The trinomial formula is a more advanced method for factoring trinomials. It involves using the formula:

x^2 + bx + c = (x + d)(x + e)

where d and e are the roots of the quadratic equation.

For example, let’s factor the trinomial x^2 + 5x + 6 using the trinomial formula:

• Find the roots of the quadratic equation: x^2 + 5x + 6 = 0
• Use the quadratic formula to find the roots: x = (-b ± √(b^2 - 4ac)) / 2a
• Simplify the roots: x = (-5 ± √(5^2 - 4*1*6)) / 2*1 = (-5 ± √(25 - 24)) / 2 = (-5 ± √1) / 2
• Simplify the roots further: x = (-5 ± 1) / 2
• Write the trinomial as the product of two binomials: x^2 + 5x + 6 = (x + (-5 + 1)/2)(x + (-5 - 1)/2) = (x + -2)(x + -3) = (x - 2)(x - 3)

📝 Note: The trinomial formula is a more advanced method and is not recommended for beginners.

Method 5: Using Online Tools

There are many online tools available that can help you factor trinomials, such as factoring calculators and algebra software. These tools can be very helpful, especially for more complex trinomials.

However, it’s always best to try to factor trinomials on your own first, using one of the methods above. This will help you understand the underlying math and improve your problem-solving skills.

In conclusion, factoring trinomials can be a challenging task, but with the right strategies and techniques, it can be made easier. By using one or more of the methods above, you can factor trinomials with confidence and accuracy.