7 Essential Exponent Laws You Need to Know

Understanding Exponent Laws: A Comprehensive Guide
Exponent laws are a fundamental concept in mathematics, and understanding them is crucial for solving various mathematical problems. Exponents are used to represent repeated multiplication of a number by itself, and they have several laws that govern their behavior. In this article, we will discuss seven essential exponent laws that you need to know.
What are Exponent Laws?
Exponent laws are a set of rules that define how exponents behave when numbers are multiplied or divided. These laws help simplify complex expressions and make it easier to solve mathematical problems. There are several exponent laws, but we will focus on the seven most essential ones.
1. The Product of Powers Law
The product of powers law states that when you multiply two numbers with the same base, you can add their exponents. This law can be expressed as:
a^m × a^n = a^(m+n)
For example, 2^3 × 2^4 = 2^(3+4) = 2^7.
📝 Note: This law only applies when the bases are the same.
2. The Power of a Power Law
The power of a power law states that when you raise a number with an exponent to another power, you can multiply the exponents. This law can be expressed as:
(a^m)^n = a^(m×n)
For example, (2^3)^4 = 2^(3×4) = 2^12.
3. The Power of a Product Law
The power of a product law states that when you raise a product of numbers to a power, you can raise each number to that power separately. This law can be expressed as:
(ab)^m = a^m × b^m
For example, (2 × 3)^4 = 2^4 × 3^4.
4. The Quotient of Powers Law
The quotient of powers law states that when you divide two numbers with the same base, you can subtract their exponents. This law can be expressed as:
a^m ÷ a^n = a^(m-n)
For example, 2^5 ÷ 2^3 = 2^(5-3) = 2^2.
📝 Note: This law only applies when the bases are the same.
5. The Zero Exponent Law
The zero exponent law states that any number raised to the power of zero is equal to 1. This law can be expressed as:
a^0 = 1
For example, 2^0 = 1.
6. The Negative Exponent Law
The negative exponent law states that a number raised to a negative power is equal to the reciprocal of that number raised to the positive power. This law can be expressed as:
a^(-m) = 1/a^m
For example, 2^(-3) = 1⁄2^3.
7. The Rational Exponent Law
The rational exponent law states that a number raised to a rational power can be expressed as a combination of integer powers. This law can be expressed as:
a^(m/n) = (a^m)^(1/n)
For example, 2^(3⁄4) = (2^3)^(1⁄4).
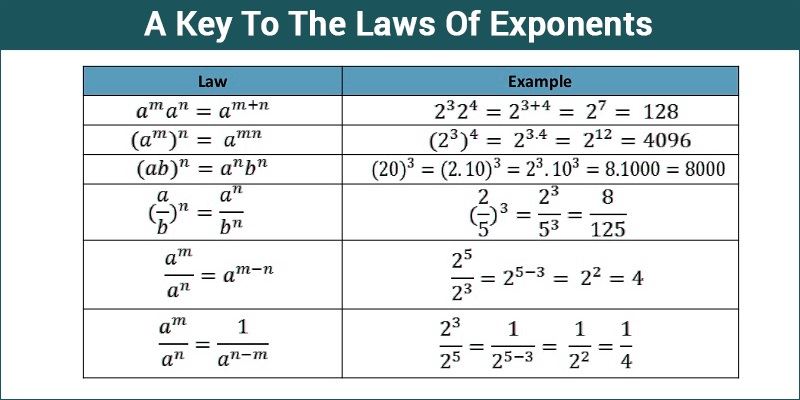
| Exponent Law | Formula | Example |
|---|---|---|
| Product of Powers | a^m × a^n = a^(m+n) | 2^3 × 2^4 = 2^7 |
| Power of a Power | (a^m)^n = a^(m×n) | (2^3)^4 = 2^12 |
| Power of a Product | (ab)^m = a^m × b^m | (2 × 3)^4 = 2^4 × 3^4 |
| Quotient of Powers | a^m ÷ a^n = a^(m-n) | 2^5 ÷ 2^3 = 2^2 |
| Zero Exponent | a^0 = 1 | 2^0 = 1 |
| Negative Exponent | a^(-m) = 1/a^m | 2^(-3) = 1/2^3 |
| Rational Exponent | a^(m/n) = (a^m)^(1/n) | 2^(3/4) = (2^3)^(1/4) |
In conclusion, understanding exponent laws is crucial for solving various mathematical problems. By applying these seven essential exponent laws, you can simplify complex expressions and make it easier to solve mathematical problems. Remember to practice using these laws to become more proficient in using them.
What are exponent laws?
+Exponent laws are a set of rules that define how exponents behave when numbers are multiplied or divided.
What is the product of powers law?
+The product of powers law states that when you multiply two numbers with the same base, you can add their exponents.
What is the zero exponent law?
+The zero exponent law states that any number raised to the power of zero is equal to 1.
How do I apply exponent laws to solve mathematical problems?
+To apply exponent laws, identify the type of problem you are solving and choose the relevant exponent law to apply. Simplify the expression using the chosen law and solve the problem.
Why are exponent laws important?
+Exponent laws are important because they help simplify complex expressions and make it easier to solve mathematical problems.