7 Ways to Master Equivalent Ratios
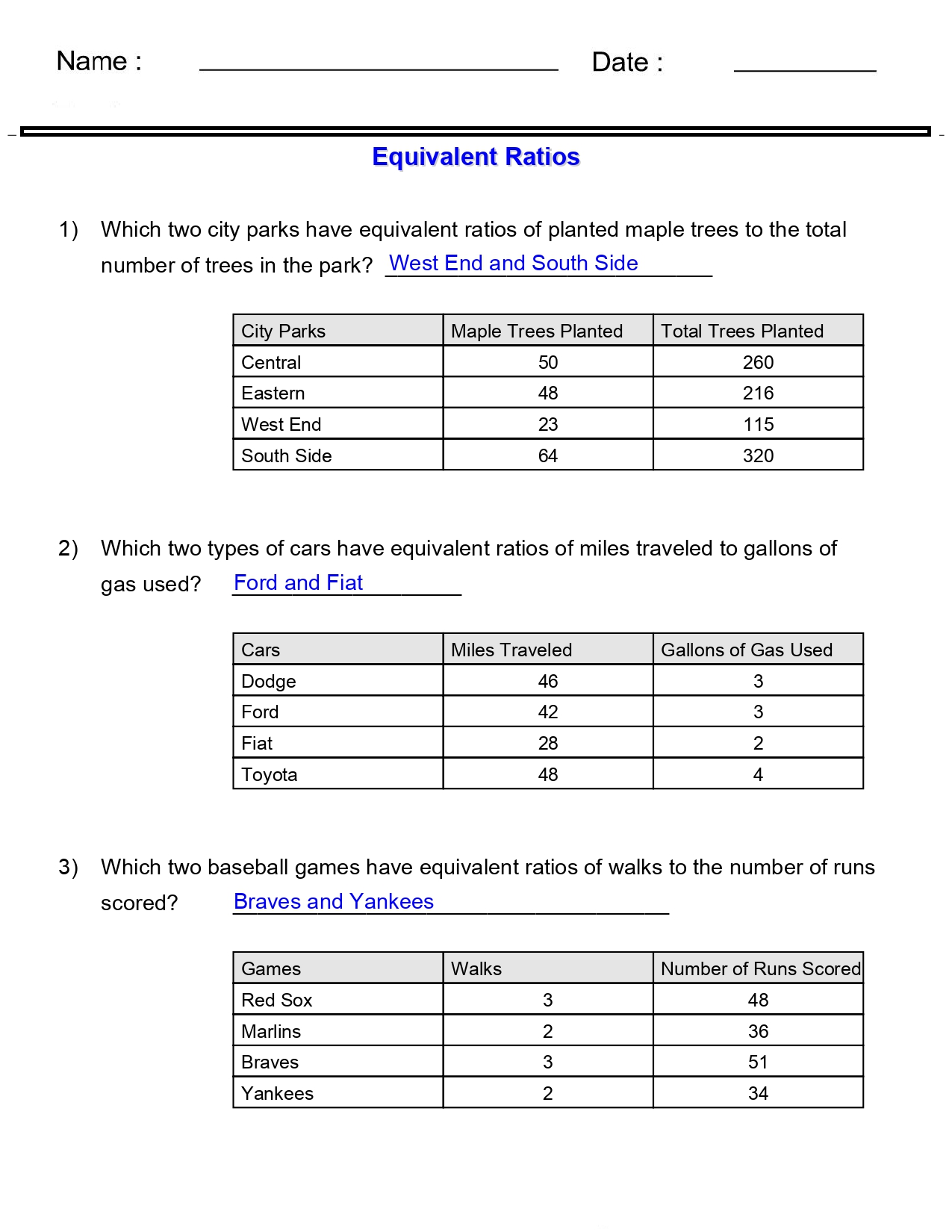
Unlocking the Power of Equivalent Ratios
Equivalent ratios are a fundamental concept in mathematics, and mastering them is essential for problem-solving in various mathematical disciplines, including algebra, geometry, and trigonometry. In this article, we will explore seven ways to master equivalent ratios, providing you with a comprehensive understanding of this crucial mathematical concept.
What are Equivalent Ratios?
Before diving into the ways to master equivalent ratios, let’s first define what they are. Equivalent ratios are ratios that have the same value or proportion. In other words, two ratios are equivalent if they represent the same relationship between two quantities. For example, 1:2 and 2:4 are equivalent ratios because they both represent the same proportion.
Way #1: Simplifying Ratios
One of the simplest ways to master equivalent ratios is to simplify them. Simplifying a ratio involves dividing both numbers by their greatest common divisor (GCD). For instance, the ratio 4:6 can be simplified by dividing both numbers by 2, resulting in the equivalent ratio 2:3.
Example:

| Ratio | Simplified Ratio |
|---|---|
| 4:6 | 2:3 |
| 6:8 | 3:4 |
| 8:10 | 4:5 |
Way #2: Multiplying and Dividing Ratios
Another way to master equivalent ratios is to multiply and divide them. When you multiply or divide a ratio by a number, you are essentially scaling the ratio. For example, multiplying the ratio 2:3 by 2 results in the equivalent ratio 4:6.
Example:
| Ratio | Multiplied Ratio | Divided Ratio |
|---|---|---|
| 2:3 | 4:6 (x2) | 1:1.5 (÷2) |
| 3:4 | 6:8 (x2) | 1.5:2 (÷2) |
| 4:5 | 8:10 (x2) | 2:2.5 (÷2) |
📝 Note: When multiplying or dividing a ratio, make sure to perform the operation on both numbers to maintain the equivalent ratio.
Way #3: Identifying Equivalent Ratios
To master equivalent ratios, it’s essential to be able to identify them. One way to do this is to look for ratios that have the same proportion or value. For example, the ratios 1:2, 2:4, and 3:6 are all equivalent because they represent the same proportion.
Example:
| Ratio | Equivalent Ratios |
|---|---|
| 1:2 | 2:4, 3:6, 4:8 |
| 2:3 | 4:6, 6:9, 8:12 |
| 3:4 | 6:8, 9:12, 12:16 |
Way #4: Creating Equivalent Ratios
Creating equivalent ratios is another way to master them. To create an equivalent ratio, you can multiply or divide a ratio by a number. For example, multiplying the ratio 2:3 by 3 results in the equivalent ratio 6:9.
Example:
| Ratio | Equivalent Ratio |
|---|---|
| 2:3 | 6:9 (x3) |
| 3:4 | 9:12 (x3) |
| 4:5 | 12:15 (x3) |
Way #5: Using Real-World Examples
Using real-world examples is an excellent way to master equivalent ratios. Real-world examples can help you understand the practical applications of equivalent ratios and make them more relatable. For instance, equivalent ratios can be used in cooking, where a recipe might call for a certain proportion of ingredients.
Example:
A recipe calls for a ratio of 2:3 of flour to sugar. If you want to make a larger batch, you can multiply the ratio by 2, resulting in the equivalent ratio 4:6.
Way #6: Practicing with Word Problems
Practicing with word problems is another effective way to master equivalent ratios. Word problems can help you apply equivalent ratios to real-world scenarios and develop your problem-solving skills. For example:
Example:
Tom has a recipe for making cookies that calls for a ratio of 2:3 of butter to sugar. If he wants to make a double batch, what is the equivalent ratio of butter to sugar?
Way #7: Using Visual Aids
Using visual aids such as diagrams, charts, and graphs can help you master equivalent ratios. Visual aids can make it easier to understand and compare equivalent ratios. For example, you can use a graph to plot equivalent ratios and visualize their relationships.
Example:
A graph can be used to plot equivalent ratios, such as 1:2, 2:4, and 3:6, to visualize their relationships and show that they are equivalent.
By mastering equivalent ratios, you can improve your problem-solving skills and apply mathematical concepts to real-world situations. Remember to simplify ratios, multiply and divide them, identify equivalent ratios, create equivalent ratios, use real-world examples, practice with word problems, and use visual aids to become proficient in equivalent ratios.
In conclusion, mastering equivalent ratios is a fundamental skill in mathematics that can be achieved with practice, patience, and persistence. By following these seven ways to master equivalent ratios, you can develop a deeper understanding of this crucial mathematical concept and apply it to various mathematical disciplines.
What are equivalent ratios?
+Equivalent ratios are ratios that have the same value or proportion.
How can I simplify a ratio?
+You can simplify a ratio by dividing both numbers by their greatest common divisor (GCD).
Can I multiply and divide ratios?
+Yes, you can multiply and divide ratios to scale them. However, make sure to perform the operation on both numbers to maintain the equivalent ratio.