5 Ways to Master Piecewise Functions

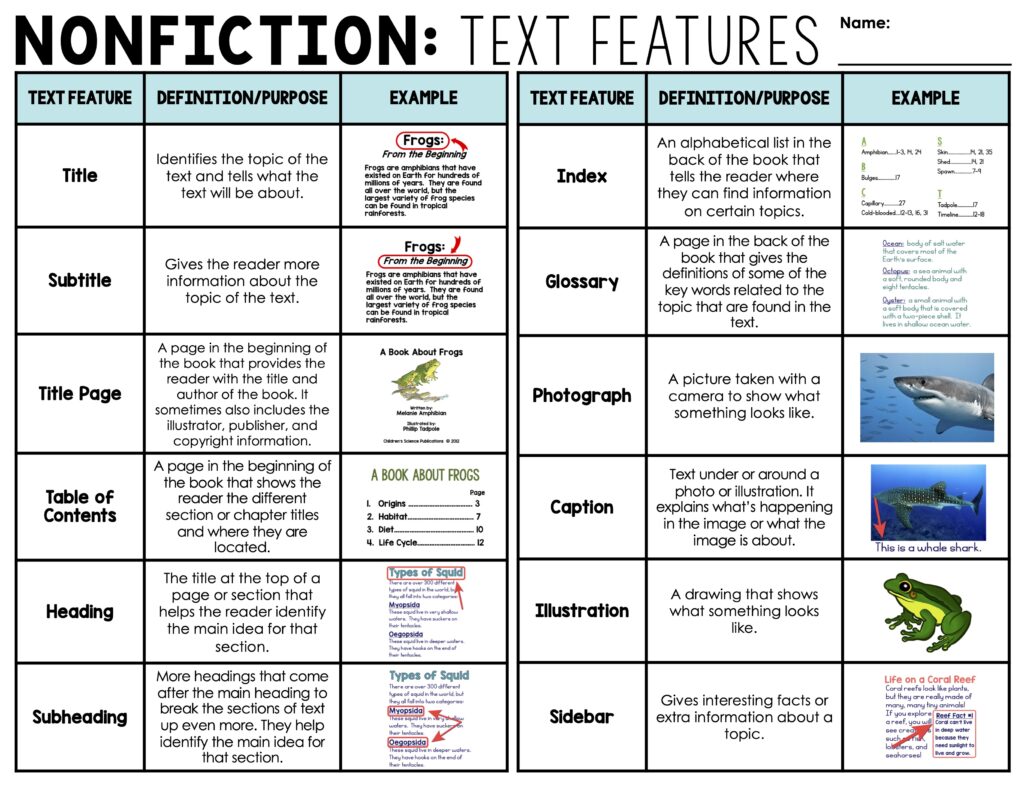
Understanding Piecewise Functions

Piecewise functions are a fundamental concept in mathematics, and they can be a bit tricky to master. A piecewise function is a function that is defined by multiple sub-functions, each applied to a specific interval of the domain. In other words, the function behaves differently on different parts of its domain. In this article, we will explore five ways to master piecewise functions.

1. Learn the Notation

The first step to mastering piecewise functions is to learn the notation. Piecewise functions are typically denoted using the following syntax:

f(x) = {
  f_1(x) & x ∈ D_1
  f_2(x) & x ∈ D_2
 ...
  f_n(x) & x ∈ D_n
}

Where f_1(x), f_2(x),…, f_n(x) are the sub-functions, and D_1, D_2,…, D_n are the intervals of the domain.

💡 Note: The notation may vary depending on the context, but the idea remains the same.

2. Visualize the Graph

Visualizing the graph of a piecewise function can help you understand its behavior. Each sub-function corresponds to a specific part of the graph. By plotting the graph, you can see how the function behaves on different intervals.

Here’s an example of a piecewise function:

f(x) = {
  x^2 & x < 0
  x + 1 & x ≥ 0
}

By plotting the graph, you can see that the function is a parabola for x < 0 and a straight line for x ≥ 0.

3. Practice Simplifying Piecewise Functions

Simplifying piecewise functions can help you understand their structure and behavior. To simplify a piecewise function, you need to find a common expression for the sub-functions.

For example, consider the following piecewise function:

f(x) = {
  x^2 + 1 & x < 0
  x^2 - 1 & x ≥ 0
}

By factoring out the common term x^2, you can simplify the function to:

f(x) = x^2 + {
  1 & x < 0
  -1 & x ≥ 0
}

📝 Note: Simplifying piecewise functions can help you identify patterns and relationships between the sub-functions.

4. Learn to Graph Piecewise Functions

Graphing piecewise functions can be a bit tricky, but with practice, you can become proficient. Here are some steps to graph a piecewise function:

1. Identify the sub-functions and their corresponding intervals.
2. Plot the graph of each sub-function on its corresponding interval.
3. Combine the graphs to form the complete graph of the piecewise function.

Here’s an example of a piecewise function and its graph:

f(x) = {
  x^2 & x < 0
  x + 1 & x ≥ 0
}

The graph of the function is a parabola for x < 0 and a straight line for x ≥ 0.

5. Apply Piecewise Functions to Real-World Problems

Piecewise functions have many real-world applications, such as modeling population growth, electrical circuits, and mechanical systems. By applying piecewise functions to real-world problems, you can develop a deeper understanding of their behavior and significance.

For example, consider a population growth model that uses a piecewise function to describe the growth rate:

P(t) = {
  2t & t < 10
  3t - 10 & t ≥ 10
}

This function describes the population growth rate as a linear function for the first 10 years and a quadratic function thereafter.

📊 Note: Applying piecewise functions to real-world problems can help you develop problem-solving skills and critical thinking.

To summarize, mastering piecewise functions requires a combination of understanding the notation, visualizing the graph, simplifying the function, learning to graph the function, and applying the function to real-world problems. By following these steps, you can develop a deeper understanding of piecewise functions and their significance in mathematics.

In conclusion, piecewise functions are a powerful tool in mathematics, and mastering them can help you develop problem-solving skills and critical thinking. By following the steps outlined in this article, you can become proficient in working with piecewise functions and apply them to real-world problems.