5 Easy Ways to Divide Fractions by Whole Numbers

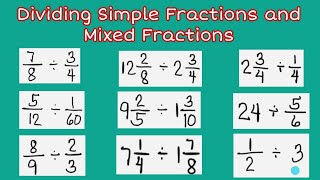
Dividing Fractions by Whole Numbers: A Simplified Approach

Dividing fractions by whole numbers can seem daunting, but with the right approach, it can be simplified. In this article, we’ll explore five easy ways to divide fractions by whole numbers, making it easier for you to tackle math problems with confidence.

Method 1: Inverting and Multiplying

One of the most common methods for dividing fractions by whole numbers is to invert the fraction and multiply. This involves flipping the fraction (i.e., swapping the numerator and denominator) and then multiplying it by the whole number.

For example, let’s divide ¹⁄₂ by 3:

🤔 Note: When dividing fractions, we need to invert the fraction and multiply by the reciprocal of the whole number.

¹⁄₂ ÷ 3 = ¹⁄₂ × ¹⁄₃ = ¹⁄₆

Method 2: Converting to Equivalent Fractions

Another way to divide fractions by whole numbers is to convert the fraction to an equivalent fraction with a denominator that is a multiple of the whole number.

For instance, let’s divide ³⁄₄ by 2:

³⁄₄ = ⁶⁄₈ ( multiplying numerator and denominator by 2)

Now, we can divide ⁶⁄₈ by 2:

⁶⁄₈ ÷ 2 = 6 ÷ 2 / 8 = ³⁄₈

Method 3: Using Visual Aids

Visual aids like number lines, fraction strips, or circles can help you understand the concept of dividing fractions by whole numbers. By representing the fraction and whole number visually, you can see the division process more clearly.

For example, let’s divide ²⁄₃ by 4 using a number line:

Imagine a number line with 0, ¹⁄₃, ²⁄₃, ³⁄₃, and so on. We want to divide ²⁄₃ by 4, so we need to find ¹⁄₄ of ²⁄₃.

By visualizing the number line, we can see that ¹⁄₄ of ²⁄₃ is equal to ¹⁄₆.

Method 4: Simplifying Before Dividing

Sometimes, it’s easier to simplify the fraction before dividing it by a whole number. This involves reducing the fraction to its simplest form.

For example, let’s divide ⁴⁄₆ by 2:

First, simplify the fraction:

⁴⁄₆ = ²⁄₃ ( dividing numerator and denominator by 2)

Now, divide ²⁄₃ by 2:

²⁄₃ ÷ 2 = ¹⁄₃

Method 5: Using Real-World Examples

Using real-world examples can make dividing fractions by whole numbers more relatable and easier to understand. By applying math to everyday situations, you can see the practical application of division.

For instance, let’s say you have ³⁄₄ of a pizza and you want to divide it among 4 people:

³⁄₄ ÷ 4 = ³⁄₁₆ ( each person gets ³⁄₁₆ of the pizza)

By using real-world examples, you can make dividing fractions by whole numbers more accessible and fun.

📝 Note: When dividing fractions by whole numbers, make sure to simplify the fraction before dividing, if possible.

In conclusion, dividing fractions by whole numbers doesn’t have to be complicated. By using these five easy methods, you can tackle math problems with confidence and accuracy. Remember to invert and multiply, convert to equivalent fractions, use visual aids, simplify before dividing, and apply real-world examples to make dividing fractions by whole numbers a breeze.