7 Ways to Master Decimal Place Value
Mastering Decimal Place Value: A Comprehensive Guide
Decimal place value is a fundamental concept in mathematics that can be tricky to grasp, especially for students. Understanding decimal place value is crucial for performing arithmetic operations, converting between fractions and decimals, and solving real-world problems. In this article, we will explore seven ways to master decimal place value, along with practical examples and tips to reinforce your learning.
1. Understanding the Basics of Decimal Place Value
To begin with, it’s essential to understand the basics of decimal place value. A decimal number is a number that has a fractional part separated from the whole number part by a decimal point. The digits to the left of the decimal point represent the whole number part, while the digits to the right represent the fractional part.
For example, in the decimal number 45.67, the digits 45 represent the whole number part, and the digits 67 represent the fractional part.
📝 Note: The decimal point is a critical component of a decimal number, as it separates the whole number part from the fractional part.
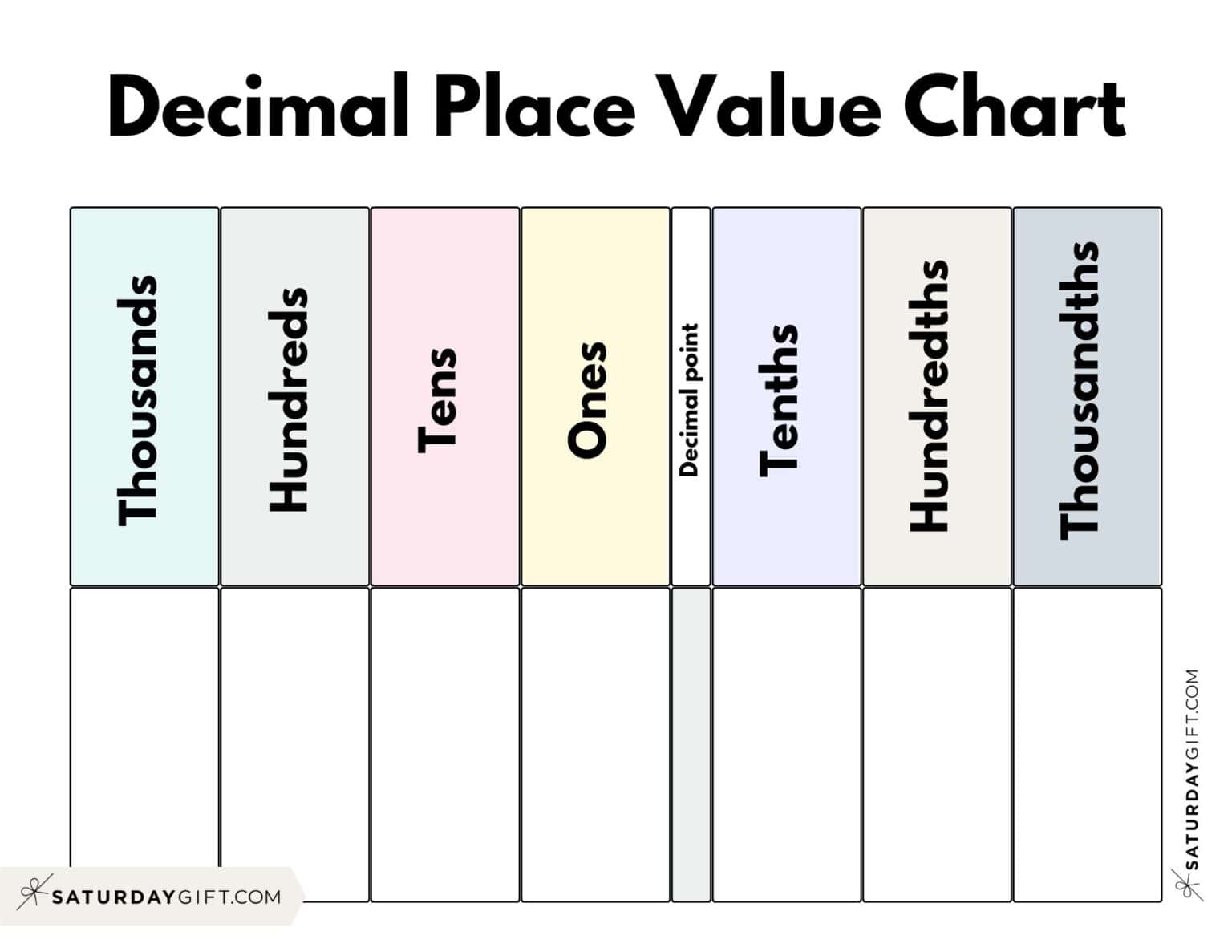
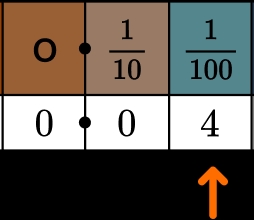
2. Learning the Place Value of Each Digit
Each digit in a decimal number has a specific place value, which determines its value in relation to the other digits. The place value of each digit can be determined by its position relative to the decimal point.
| Digit Position | Place Value |
|---|---|
| Left of the decimal point | Ones, Tens, Hundreds, etc. |
| Right of the decimal point | Tenths, Hundredths, Thousandths, etc. |
For example, in the decimal number 45.67, the place value of each digit is:
- 4: Tens
- 5: Ones
- 6: Tenths
- 7: Hundredths
3. Converting Between Fractions and Decimals
Converting between fractions and decimals is an essential skill for mastering decimal place value. To convert a fraction to a decimal, divide the numerator by the denominator.
For example, to convert the fraction 3⁄4 to a decimal, divide 3 by 4:
3 ÷ 4 = 0.75
To convert a decimal to a fraction, write the decimal as a fraction with the denominator being a power of 10.
For example, to convert the decimal 0.75 to a fraction, write:
0.75 = 75⁄100 = 3⁄4
4. Rounding Decimals to the Nearest Place Value
Rounding decimals to the nearest place value is a crucial skill in mathematics and real-world applications. To round a decimal to the nearest place value, look at the digit to the right of the place value you want to round to.
For example, to round 45.67 to the nearest tenth, look at the digit to the right of the tenths place, which is 7. Since 7 is greater than or equal to 5, round up to 45.7.
5. Adding and Subtracting Decimals with Different Place Values
Adding and subtracting decimals with different place values requires careful attention to the place value of each digit.
For example, to add 45.67 and 23.45, align the decimal points and add:
45.67
+23.45
69.12
6. Multiplying and Dividing Decimals by Powers of 10
Multiplying and dividing decimals by powers of 10 is an essential skill for mastering decimal place value. To multiply a decimal by a power of 10, move the decimal point to the right by the number of places indicated by the power of 10.
For example, to multiply 45.67 by 100, move the decimal point 2 places to the right:
45.67 × 100 = 4567.00
To divide a decimal by a power of 10, move the decimal point to the left by the number of places indicated by the power of 10.
For example, to divide 4567.00 by 100, move the decimal point 2 places to the left:
4567.00 ÷ 100 = 45.67
7. Real-World Applications of Decimal Place Value
Decimal place value has numerous real-world applications in finance, science, engineering, and everyday life. Understanding decimal place value is essential for:
- Financial transactions: calculating interest rates, investment returns, and currency conversions
- Scientific measurements: calculating distances, temperatures, and quantities
- Engineering: designing and building structures, calculating stresses and loads
- Everyday life: calculating prices, discounts, and quantities
By mastering decimal place value, you will be better equipped to tackle real-world problems and make informed decisions in your personal and professional life.
In conclusion, mastering decimal place value is a critical skill for success in mathematics and real-world applications. By following these seven steps and practicing regularly, you will develop a deep understanding of decimal place value and be able to apply it with confidence in various contexts.
What is the place value of the digit 5 in the decimal number 45.67?
+The place value of the digit 5 in the decimal number 45.67 is Ones.
How do you convert the fraction 3⁄4 to a decimal?
+To convert the fraction 3⁄4 to a decimal, divide the numerator by the denominator: 3 ÷ 4 = 0.75.
What is the result of rounding 45.67 to the nearest tenth?
+The result of rounding 45.67 to the nearest tenth is 45.7.



