5 Ways to Master Linear Functions Comparison
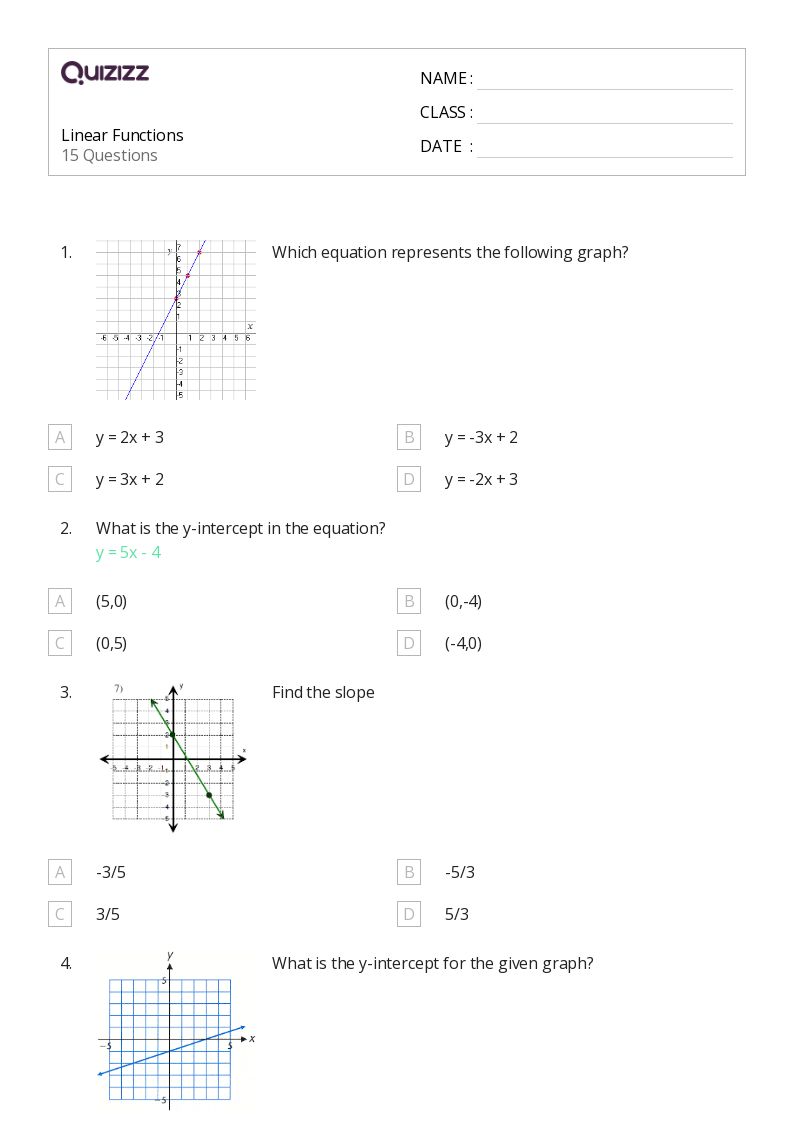
Understanding Linear Functions Comparison
Linear functions are a fundamental concept in mathematics, and comparing them is a crucial skill to master. Linear functions comparison involves analyzing and comparing the slopes, y-intercepts, and overall behavior of two or more linear functions. This skill is essential in various fields, including physics, engineering, economics, and computer science. In this article, we will explore five ways to master linear functions comparison.
1. Visualizing Linear Functions
Visualizing linear functions is an effective way to compare them. By graphing two or more linear functions on the same coordinate plane, you can quickly identify their similarities and differences. To visualize linear functions, you can use a graphing calculator or software. Here are some tips to keep in mind:
- Choose a suitable window: Make sure the window is large enough to display all the functions clearly.
- Use different colors: Use different colors to distinguish between the functions.
- Label the axes: Label the x and y axes clearly.
- Show the equations: Display the equations of the functions on the graph.
By visualizing linear functions, you can compare their:
- Slopes: The slope of a linear function represents its rate of change. By comparing the slopes, you can determine which function increases or decreases faster.
- Y-intercepts: The y-intercept represents the point where the function crosses the y-axis. By comparing the y-intercepts, you can determine which function starts higher or lower.
- Overall behavior: By comparing the overall shape of the functions, you can determine which function is more steep or more flat.
📝 Note: Visualizing linear functions can be done using various tools, including graphing calculators, software, or even online graphing tools.
2. Comparing Slopes and Y-Intercepts
Comparing the slopes and y-intercepts of linear functions is a straightforward way to compare them. Here are some tips to keep in mind:
- Slope comparison: Compare the slopes of the functions by subtracting one slope from the other. If the result is positive, the first function is steeper. If the result is negative, the second function is steeper.
- Y-intercept comparison: Compare the y-intercepts of the functions by subtracting one y-intercept from the other. If the result is positive, the first function starts higher. If the result is negative, the second function starts higher.
By comparing the slopes and y-intercepts, you can determine which function:
- Increases or decreases faster: By comparing the slopes, you can determine which function increases or decreases faster.
- Starts higher or lower: By comparing the y-intercepts, you can determine which function starts higher or lower.
📝 Note: Comparing slopes and y-intercepts can be done using algebraic methods or graphical methods.
3. Using Tables of Values
Using tables of values is another way to compare linear functions. By creating a table of values for each function, you can compare their corresponding x and y values. Here are some tips to keep in mind:
- Choose a range of x values: Choose a range of x values that covers the desired interval.
- Calculate corresponding y values: Calculate the corresponding y values for each function using the equations.
- Compare the y values: Compare the y values for each function to determine which function is higher or lower.
By using tables of values, you can compare the:
- Corresponding y values: By comparing the corresponding y values, you can determine which function is higher or lower.
- Rates of change: By comparing the rates of change, you can determine which function increases or decreases faster.
📝 Note: Using tables of values can be time-consuming, but it can be an effective way to compare linear functions.
4. Using Linear Function Properties
Using linear function properties is another way to compare linear functions. Here are some properties to keep in mind:
- Slope-intercept form: Compare the slope-intercept form of each function to determine their slopes and y-intercepts.
- Standard form: Compare the standard form of each function to determine their x and y coefficients.
- Axis of symmetry: Compare the axis of symmetry of each function to determine their symmetry.
By using linear function properties, you can compare the:
- Slopes and y-intercepts: By comparing the slope-intercept form, you can determine which function has a higher or lower slope and y-intercept.
- Symmetry: By comparing the axis of symmetry, you can determine which function is symmetric about the x or y axis.
📝 Note: Using linear function properties can be an efficient way to compare linear functions.
5. Using Real-World Applications
Using real-world applications is another way to compare linear functions. By applying linear functions to real-world scenarios, you can compare their:
- Rates of change: By comparing the rates of change, you can determine which function increases or decreases faster.
- Starting values: By comparing the starting values, you can determine which function starts higher or lower.
Here is an example of a real-world application:
| Time (hours) | Distance (miles) | Function 1 | Function 2 |
|---|---|---|---|
| 0 | 0 | y = 2x | y = 3x |
| 1 | 2 | y = 2(1) | y = 3(1) |
| 2 | 4 | y = 2(2) | y = 3(2) |
By using real-world applications, you can compare linear functions in a more meaningful way.
As we conclude, comparing linear functions is a crucial skill to master. By using the five methods outlined above, you can compare linear functions effectively and make informed decisions.
What is the best way to compare linear functions?
+The best way to compare linear functions depends on the context and the information given. However, using a combination of visualizing linear functions, comparing slopes and y-intercepts, using tables of values, using linear function properties, and using real-world applications can provide a comprehensive understanding of the functions.
How do I determine which linear function is steeper?
+To determine which linear function is steeper, compare the slopes of the functions. If the slope of one function is greater than the slope of the other function, then the first function is steeper.
Can I use real-world applications to compare linear functions?
+Yes, you can use real-world applications to compare linear functions. By applying linear functions to real-world scenarios, you can compare their rates of change, starting values, and overall behavior.
Related Terms:
- Comparing linear functions worksheet PDF
- Comparing quadratic functions worksheet pdf
- Comparing functions practice
- Comparing functions word problems